Mixture Fraction¶

• References
  • Peters 172-176
  • Poinsot 84-86
  • Smith 322-326
  • H. Pitsch and N. Peters "A consistent flamelet formulation for nonpremixed combustion considering differential diffusion effects," Combustion and Flame 114:26-40 (1998)

Notation¶

• $\xi$, $f$, $Z$ are common symbols for mixture fraction. Here, we'll use $\xi$.

Definition¶

• Mixture fraction is relevant when considering the mixing of two streams.
  • The streams are typically a fuel and an oxidizer (fuel and air).
    • It is possible to have inerts like $CO_2$ or $N_2$ in either stream.
    • It is possible to have oxidizer in both streams, or to have oxygen as part of the fuel (as in coal).
  • Can be generalized to more than two streams, in which more than one mixture fraction variable is used.
  • Normally $\xi=0$ in the oxidizer stream and $\xi=1$ in the fuel stream.
• $\xi$ is the local mass fraction of material that originated in the fuel stream:

$$\xi = \frac{m_f}{m_f + m_a}$$ $$0\le\xi\le 1$$

Mixing¶

• $\xi$ defines a linear state of mixing between two streams.
  • This is true for conserved quantities (termed conserved scalars), like elemental masses, or for species in the absence of reaction.
• Conserved scalars are elemental masses, enthalpy (in the absence of heat losses), and linear combinations of these.
• Consider elemental carbon. Denote FS as "fuel stuff" (meaning mass that originated in the $\xi=1$ stream), and AS as "air stuff" (meaning mass that originated in the $\xi=0$ stream).

$$y_C = \frac{m_C}{m_{tot}} = \frac{\text{(mass of C from AS)}+\text{(mass of C from FS)}}{m_{tot}} = \frac{m_{AS}}{m_{tot}}\left(\frac{m_C}{m_{AS}}\right) + \frac{m_{FS}}{m_{tot}}\left(\frac{m_C}{m_{FS}}\right), $$$$y_C = (1-\xi)y_{C,\xi=0} + (\xi)y_{C,\xi=1}.$$

• In general, simple mixing (no reaction) of some scalar $\psi$ is given by

$$\psi = (1-\xi)\psi_{\xi=0} + (\xi)\psi_{\xi=1}.$$ * We can rearrange the above expression to give: $$\xi = \frac{\psi-\psi_{\xi=0}}{\psi_{\xi=1}-\psi_{\xi=0}}.$$

• This shows that $\xi$ is a centered and scaled version of $\psi$ that varies between 0 and 1.

Relation to Equivalence Ratio¶

• Equivalence ratio:

$$\Phi = \frac{F/A}{(F/A)_{stoic}}$$

• Mixture fraction (mass basis):

$$\xi = \frac{F}{F+A} = \frac{F/A}{F/A + 1} = \frac{\Phi(F/A)_{st}}{\Phi(F/A)_{st}+1} \rightarrow \Phi = \frac{\xi}{1-\xi}\frac{1}{(F/A)_{st}}$$

But $$\xi_{st} = \frac{(F/A)_{st}}{(F/A)_{st}+1} \rightarrow (F/A)_{st} = \frac{\xi_{st}}{1-\xi_{st}}\rightarrow$$

$$\Phi = \frac{\xi(1-\xi_{st})}{\xi_{st}(1-\xi)}$$ $$\xi = \frac{\Phi}{\Phi + (A/F)_{st}}$$

Problems¶

Assume we have defined the composition of the streams.

1. Given stream definitions, find $\xi_{st}$.
2. Given $\xi$, find an unreacted composition.
3. Given a composition (nominally reacted), find the corresponding $\xi$.

Relation to Flames¶

• A flame consists of mixing and reaction of fuel and oxidizer streams.
• The result is a temperature and a composition (mass fractions of all species) at any location.
• Find the mixture fraction at any location given the mass fractions at the location.
  • The mixture fraction you compute will depend on the definition you use. That is, which conserved scalar you choose for $\psi$.
  • Why?

Differential diffusion (DD)¶

• Chemical reaction mixes mass from the fuel and oxidizer streams.
• Each species has it's own diffusivity.
• Diffusion can change the local ratio of elements to be different than what would be expected based on pure mixing.

Example¶

• Consider a hydrogen flame with
  • $\xi=0$ is equal moles $O_2$, $N_2$.
  • $\xi=1$ is pure hydrogen
• At the stoichiometric point we have:

$$2H_2 + O_2 + N_2\rightarrow 2H_2O + N_2$$

• The elemental mass fractions are:

\begin{align} y_H &= \frac{4}{64} = 0.0625\\ y_O &= \frac{32}{64} = 0.5\\ y_N &= \frac{28}{64} = 0.04375 \end{align}

• The mixture fractions computed using $\psi=y_H$, $\psi=y_O$, or $\psi=y_N$ will all be the same.
• Now, suppose we start with this product mixture, but allow some $H_2$ to diffuse over from a nearby fuel-rich region. Let this $H_2$ displace an equal mass of $N_2$.
  • Say we add 0.01 of $y_H$ in the form of $H_2$, and remove 0.01 of $y_N$.
  • Then $y_H$ and $y_N$ are different, but $y_O$ is the same.
  • The mixture fractions we compute using $\psi=y_H$, $\psi=y_O$, or $\psi=y_N$ will all be different, even though we are considering a single composition at a single point.

Mixture fraction is not unique in the presence of differential diffusion.

• Note, you can still go from $\xi\rightarrow y_k$ as unreacted mixing simply by using the stream definitions.
• But you can't uniquely go from $y_k\rightarrow\xi$ in the presence of DD.

Example¶

A direct simulation of a turbulent ethylene jet flame was computing with differential diffusion. 19 species were tracked. At every point in the flame the mass fractions of all species were computed and various mixture fractions computed. These are shown in the parity plot below, where each mixture fraction is plotted versus the carbon mixture fraction.

So, how do we choose the best definition of the mixture fraction in the presence of differential diffusion?

• In particular, we are interested in the case where a stoichiometric mixture of elements will give the stoichiometric value of $\xi$.
  • In our example, the modified mixture is not stoichiometric, but using $\psi=y_O$ will give $\xi=\xi_{st},$ which is not good.

Bilger's Mixture Fraction¶

The remedy is to choose a definition of the mixture fraction that uses a linear combination of all of the elements (well, actually $n_{el}-1$).

• Then, all the elements have to be in the stoichiometric proportion in order to get $\xi=\xi_{st}$.

There are many possible combinations, but the most popular is Bilger's definition, which is a scaled version of the definition of the conserved scalar used in the famous Burke-Shumann flame.

$$\xi = \frac{\beta-\beta_0}{\beta_1-\beta_0}.$$ \begin{align} \beta &= \sum_{k=1}^{n_{el}}\gamma_kZ_k = \gamma_CZ_C +\gamma_HZ_H +\gamma_OZ_O +\gamma_NZ_N. \end{align} where we'll use $Z_k$ as the local mass fraction of element $k$ (to more clearly distinguish it from a species mass fraction $y_i$). $$Z_k = \sum_{i=1}^{n_{sp}}\frac{a_{k,i}M_ky_i}{M_i}.$$

• Here, $a_{k,i}$ is the number of atoms of element $k$ in species $i$, and M are molecular weights.
• We consider the following combustion reaction, define $\beta=0$ at the stoichiometric point, and then choose values for the $\gamma$s:

$$C_xH_y + \left(x+\frac{y}{4}\right)O_2 + 3.76\left(x+\frac{y}{4}\right)N_2\rightarrow xCO_2 + \frac{y}{2}H_2O + 3.76\left(x+\frac{y}{4}\right)N_2.$$

• For this reaction, the $Z$s are given by

\begin{align} Z_C &= \frac{xM_C}{D}, \\ Z_H &= \frac{yM_H}{D}, \\ Z_O &= \frac{2(x+y/4)M_O}{D}, \\ Z_N &= \frac{7.52(x+y/4)M_N}{D}, \end{align}

where $D$ is the sum of all the numerators: $D = xM_C + yM_H + 2(x+y/4)M_O + 7.52(x+y/4)M_N$.

• Insert these into $\beta$:

$$\beta = 0 = \frac{\gamma_CxM_C + \gamma_HyM_H + 2\gamma_O(x+y/4)M_O + 7.52\gamma_N(x+y/4)M_N}{D}.$$

• Now, the mole numbers $x$ and $y$ are independent and arbitrary (but positive) so we need the coeffients of $x$ and $y$ to be zero.

\begin{align} x:\phantom{xxxxxx}& \gamma_CM_C + 2\gamma_OM_O + 7.52\gamma_NM_N = 0 \\ y:\phantom{xxxxxx}& \gamma_HM_H + \gamma_O\frac{M_O}{2} + \gamma_N\frac{7.52M_N}{4} = 0 \end{align}

• We have two constraint equations with four $\gamma$ parameters.
  • Let $\gamma_N=0$.
  • Then we have

\begin{align} \gamma_C &= -\frac{2\gamma_OM_O}{M_C} \\ \gamma_H &= -\frac{\gamma_OM_O}{2M_H} \end{align}

* Let $\gamma_O=-1/M_O$. 
* This gives

\begin{align} \gamma_C &= \frac{2}{M_C}, \\ \gamma_H &= \frac{1}{2M_H}, \\ \gamma_O &= -\frac{1}{M_O}, \\ \gamma_N &= 0. \end{align}

Mixture fraction transport equation¶

• The species transport equation is given by

$$\frac{\partial \rho y_i}{\partial t} + \nabla\cdot(\rho y_i\vec{v}_i) = \dot{m}'''.$$

• We write $\vec{v}_i = \vec{v}+\vec{v}_i^D$. That is, the species velocity is decomposed into a mass average velocity and a species diffusion velocity.
  • We then write $\vec{j}_i=\rho y_i\vec{v}_i^D$:

$$\frac{\partial \rho y_i}{\partial t} + \nabla\cdot(\rho y_i\vec{v}) + \nabla\cdot\vec{j}_i= \dot{m}'''.$$

• We now model $\vec{j}_i$ using a Fickian form:

$$\vec{j}_i = -\rho D_i\nabla y_i.$$

• This gives

$$\frac{\partial \rho y_i}{\partial t} + \nabla\cdot(\rho y_i\vec{v}) - \nabla\cdot(\rho D_i\nabla y_i)= \dot{m}'''.$$

• If we assume all species share the same diffusivity: $D_i=D$, then using the definition of the mixture fraction in terms of elemental mass fractions $Z_k$, we can derive the following mixture fraction transport equation:

$$\frac{\partial \rho\xi}{\partial t} + \nabla\cdot(\rho \xi\vec{v}) - \nabla\cdot(\rho D\nabla\xi) = 0.$$ * This equation neglects differential diffusion. However, it can also be used as the *definition* of the mixture fraction. That is, we could solve this transport equation to obtain $\xi(t,x,y,z)$. This could be solved along with species transport equations that may or may not involve differential diffusion. * The diffusivity used in the mixture fraction transport equation is normally taken to be the thermal diffusivity $\alpha$, since this is the enthalpy diffusivity, and enthalpy is a conserved scalar under conditions of equal species diffusivities and no radiative heat losses.

Mixture fraction as a flame coordinate¶

• It is common to plot variables like temperature versus mixture fraction rather than versus a physical coordinate.

Consider a laminar opposed jet flame:¶

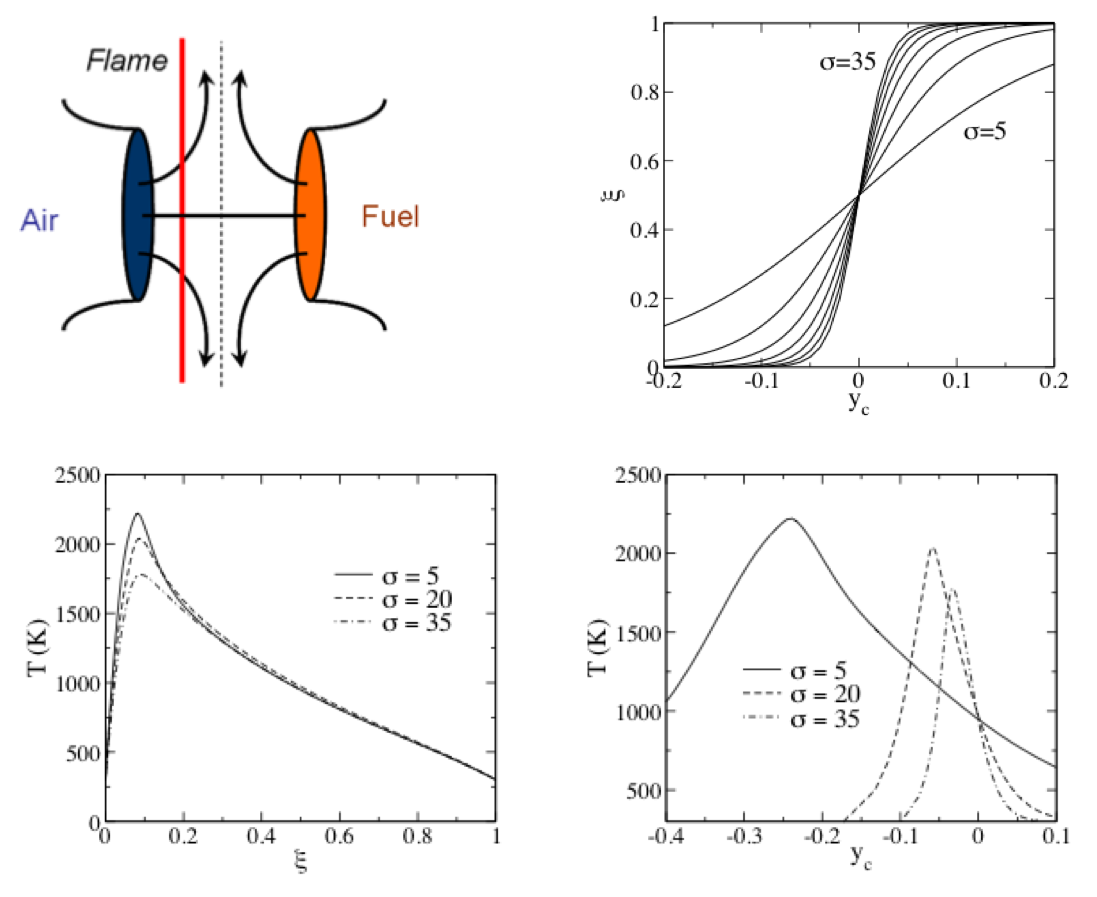
• Note that the flame lies on the oxidizer side of the centerline.
• The flow stagnates at the centerline
• The top right plot shows the mixture fraction profile versus position for various $\sigma$, where $\sigma$ is a strain rate (related to the jet velocities.
• We can plot the flame temperature versus position (here $y_c$ is position). See the lower right plot.
  • But since there is a one-to-one relation between $\xi$ and $y_c$, we can also plot temperature versus $\xi$.
  • This is done in the lower left plot.
  • Note how the curves collapse much more strongly for $T$ versus $\xi$, than for $T$ versus $y_c$.