Nonlinear equation I

• Find roots of $f(x)$. That is, find the value of $x$ so that $f(x)=0$.
• All nonlinear algebraic problems can be written in the form $f(x)=0$. Just move all terms to one side of the equation.
• Numerical methods for nonlinear problems proceed by setting an initial guess for the solution, and iterating to improve the guess until some desired error tolerance is achieved.
• Open and Closed domain methods.
• Here:
  • discuss closed domain methods
  • one equation in one unknown

Bound the solution

• Bracket the root:
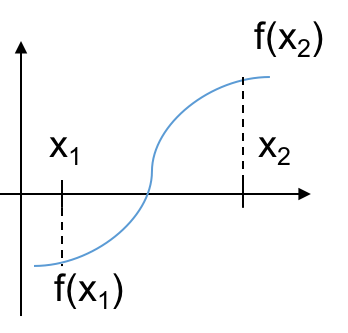
  • Choose two guesses for the solution: $x_1$ and $x_2$. If $f(x_1)\cdot f(x_2)<0$ then the two guesses bracket the root.
  • This implies that the root is between the two guesses.

Procedures

• Graph it.
  • Visual picture can be very helpful.
  • Provides an intial guess of the root.
  • Indicates the function behavior, and possible problem areas.
  • May not be practical, however.
    • Cost of function evaluation may be excessive.
• Do a simple incremental search.
  • Simply set a small $\Delta x$ and search the domain for $f(x)=0$.
  • Obviously not very practical.
• Past experience
  • Output of one problem may be a good guess for the input of another problem.
    • This especially true in cases where we do multiple solves, which is quite common.
  • Use intuition:
    • species mass fractions should be between 0 and 1.
    • most temperatures in K should be in reasonable ranges.
• Solve a simpler problem to get a guess for the harder problem.
  • For example, if solving for a nonideal gas, get an initial guess using an ideal gas.
  • Another example, if solving for temperature with a variable heat capacity, find a temperature guess using a constant heat capacity, which results in an easy linear solve for the guess.
  • In combustion, we might solve using a simple 1-step reaction mechanism, instead of a more complex 400 step mechanism.

Once you have a bracket refine the root

• Reduce the size of the interval, while maintaining the bracket.
• Two methods: bisection, and regula falsi (false position)
  • These are robust (they work!), but they are not overly fast.

Bisection

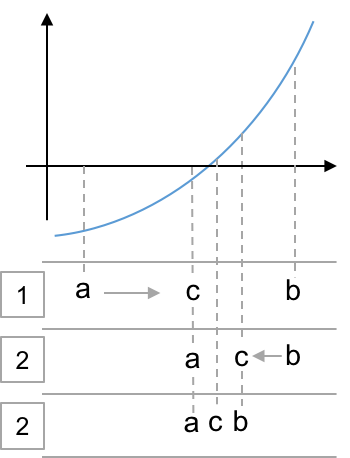
• Guess two points that bracket the root: $a$, $b$
• Check for $f(a)=0$ or $f(b)=0$
• Bracket tests:
  • $f(a)f(b)<0$
  • ($f(a)>0$ and $f(b)<0$) or ($f(a)<0$ and $f(b)>0$)
• Refine: $c = (a+b)/2$
• Select new bracket:
  • if $f(a)f(c) < 0 \rightarrow b=c$
  • else $a=c$

Error

• The error is always bounded by $\epsilon_n\le|b-a|$
• $\epsilon_{n+1} = \epsilon_n/2$ $\rightarrow$ linear convergence.
• $\epsilon_0$, $\epsilon_1=\epsilon_0/2$, $\epsilon_2 = \epsilon_1/2 = \epsilon_0/4 = \epsilon_0/2^2$
• $\rightarrow \epsilon_n = \epsilon_0/2^n$.
• Hence: $$n = \log_2\left(\frac{\epsilon_0}{\epsilon_n}\right)$$
• That is, to reduce the error from $\epsilon_0 \le |a-b|$ to some desired $\epsilon_n$ requires $n=\log_2(\epsilon_0/\epsilon_n)$ iterations.

Regula Falsi

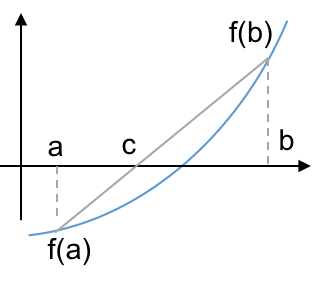
• Rather than bisect the interval to find $c$, draw an intersecting line between $f(a)$ and $f(b)$ as an approximation to the function.

• Solve the root of this linear approximation:

  • that is, where the line intersects the x-axis where $y=f(x)$ is zero.
  • Equation for the line: $$f_l(x) = f(a) + \frac{f(b)-f(a)}{b-a}(x-a).$$
  • Then let $f_l(c)=0$ and solve for $c$ to get: $$ c= a - f(a)\frac{b-a}{f(b)-f(a)}.$$

• To retain the bracket, replace $a$ or $b$ with $c$ as for bisection.

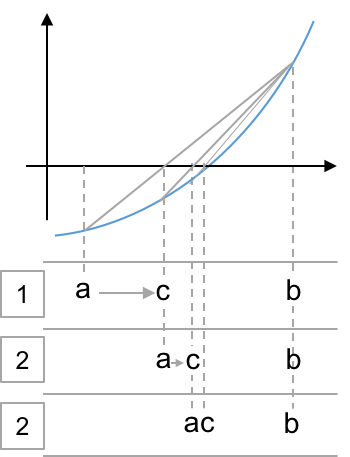
• Robust
• Usually faster than bisection
• No error bound though.
• May get superlinear convergence
  • Keeping the old versus new function evaluation…
• Consider the following case though (slow):

Convergence

• When to stop?
  • $|b-a| < \epsilon$
    • absolute error
    • works for $x=1$
    • not so good for $x=10^{20}$
  • $|b-a|/|c| < \epsilon$
    • relative error
  • $|f(c)|< \epsilon$
    • error in function versus error in root.

Consider:

• On the left, the bracket is narrow, but the function is not zero.
• On the right, the function is near zero, but the bracket is not narrow.
• Do both $|b-a|/|c| < \epsilon_1$ and $|f(c)|<\epsilon_2$.

Bisection example

Find root of $f(x)=(x-2)^2 - 1$.

function bisection(f, a, b, tol=1E-5, maxit=10000)
    
    fa = f(a)
    fb = f(b)
    
    if fa==0 return a, 0 end
    if fb==0 return b, 0 end
    
    if (fa>=0 && fb>=0) || (fa<=0 && fb<=0)
        println("Error, a and b don't bracket the root")
        return NaN, -1
    end
    
    for nit in 1:maxit
        
        c = 0.5*(a+b)
        fc = f(c)
        if fc == 0 return c, nit end
        
        if (fc > 0 && fa < 0) || (fc < 0 && fa > 0)
            b = c
            fb = fc
        else
            a = c
            fa = fc
        end

        if (abs(fc) <= tol) || (abs((b-a)/c) <= tol)
            return c, nit
        end
    end
    
    println("Warning, no convergence in $maxit iterations")
    c, maxit
end
        
#--------------------        

func1(x) = (x-2.)^2 - 1.

#--------------------        

x, nit = bisection(func1, 2., 3.5, 1E-8, 100)

println("Solution x = $x found in $nit iterations")
println("f(x) = $(func1(x))")

Solution x = 3.0000000074505806 found in 26 iterations
f(x) = 1.4901161193847656e-8

Compare with nlsolve

import NLsolve: nlsolve

function func1!(F,x)
    F[1] = (x[1] - 2.0)^2 - 1.0 
end

xguess  = [20.]
results = nlsolve(func1!, xguess)

println("Solution x = $(results.zero)")

Solution x = [3.000000000000861]