Partial differential equations (PDEs)¶
Trends¶
- Nonlinear equations $\rightarrow$ linear equations with iteration
- ODEs $\rightarrow$ algebraic (linear) equations
- PDEs $\rightarrow$ system of ODEs, or system of algebraic equations.
Definition¶
- A PDE is a differential equation with two or more independent variables (or coordinates).
- Typically $t$, $x$, $y$, $z$.
- But often more general coordinates, including state space coordinates
- Composition
- Temperature
- etc.
- The order of a PDE is the order of the highest derivative appearing in the equation.
- "A linear PDE is one in which all of the partial derivatives appear in linear form and none of the coefficients depends on the dependent variable." (Hoffman)
- The coefficients can be functions of the independent variables.
- This is analogous to linear ODEs.
Examples¶
Laplace equation: $$\frac{\partial^2f}{\partial x^2} + \frac{\partial^2f}{\partial y^2} = 0.$$
Diffusion equation: $$\frac{\partial f}{\partial t} = \alpha \frac{\partial^2f}{\partial x^2}$$
Wave equation: $$\frac{\partial f}{\partial t} = c \frac{\partial f}{\partial x}$$
Homogeneous¶
- The above examples are all homogeneous. If we add a function like $F(x,y,t)$ to the above equations, they become nonhomogeneous.
- Note that $F$ does not involve $f$.
- Nonhomogeneous terms do not change the basic behavior of the PDE, or complicate the numerical solution method.
Systems of ODEs¶
- Often we have a coupled system of ODEs.
- Examples
- Combined heat and mass transfer
- Navier-Stokes equations
- Equations of motion
- Maxwell equations
Notation¶
- Use subscripts to denote derivatives $$f_t \equiv \frac{\partial f}{\partial t}.$$ $$f_{xx} \equiv \frac{\partial^2f}{\partial x^2},$$ $$f_{xy} \equiv \frac{\partial^2f}{\partial x\partial y}.$$
Operators¶
Gradient $$ \vec{\nabla} f = \vec{i}\frac{\partial f}{\partial x} + \vec{j}\frac{\partial f}{\partial y}$$
Divergence $$ \vec{\nabla} \cdot \vec{f} = \frac{\partial f_0}{\partial x} + \frac{\partial f_1}{\partial y}$$
Laplacian $\nabla^2 \equiv \vec{\nabla}\cdot\vec{\nabla}$ $$ \nabla^2 f = \frac{\partial^2 f}{\partial x^2} + \frac{\partial^2 f}{\partial y^2}$$
(Curl)
Solution methods¶
- Finite difference method (similar to approach shown for BVPs)
- Finite volume methods
- Galerkin methods
- Finite element methods
- Spectral methods
More examples¶
Reacting Navier-Stokes equations¶

Laminar flamelet equations (with soot)¶
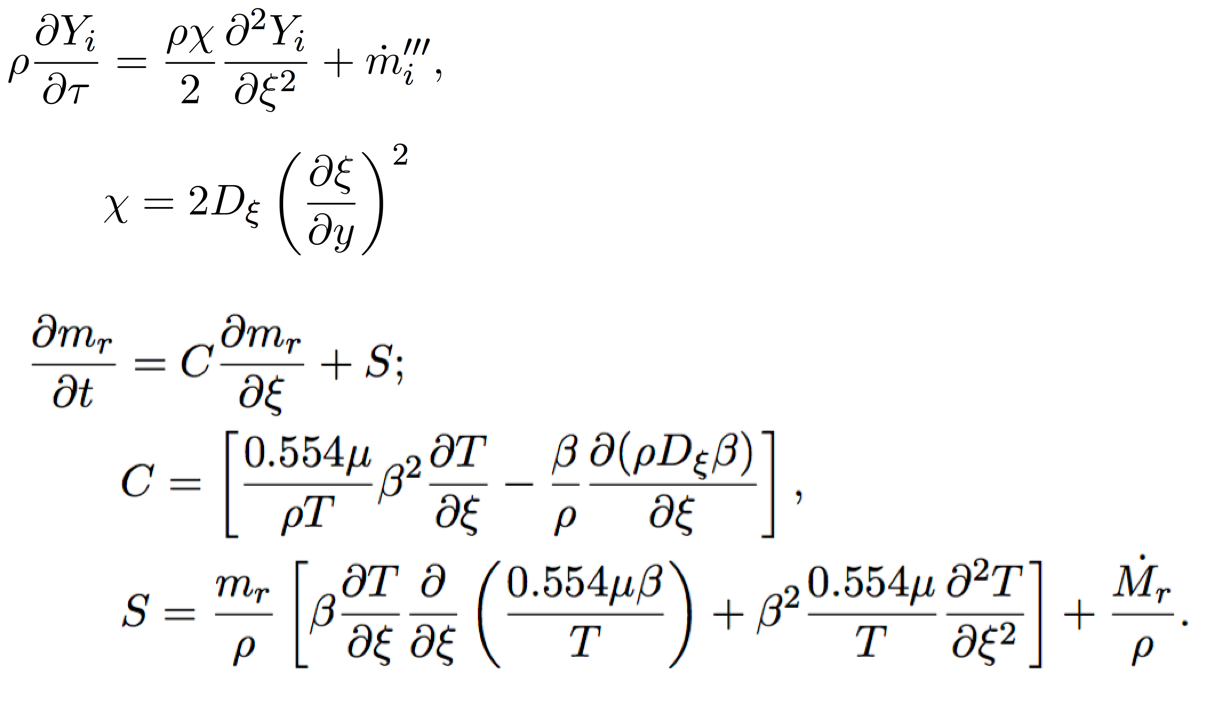
Joint PDF transport equation¶
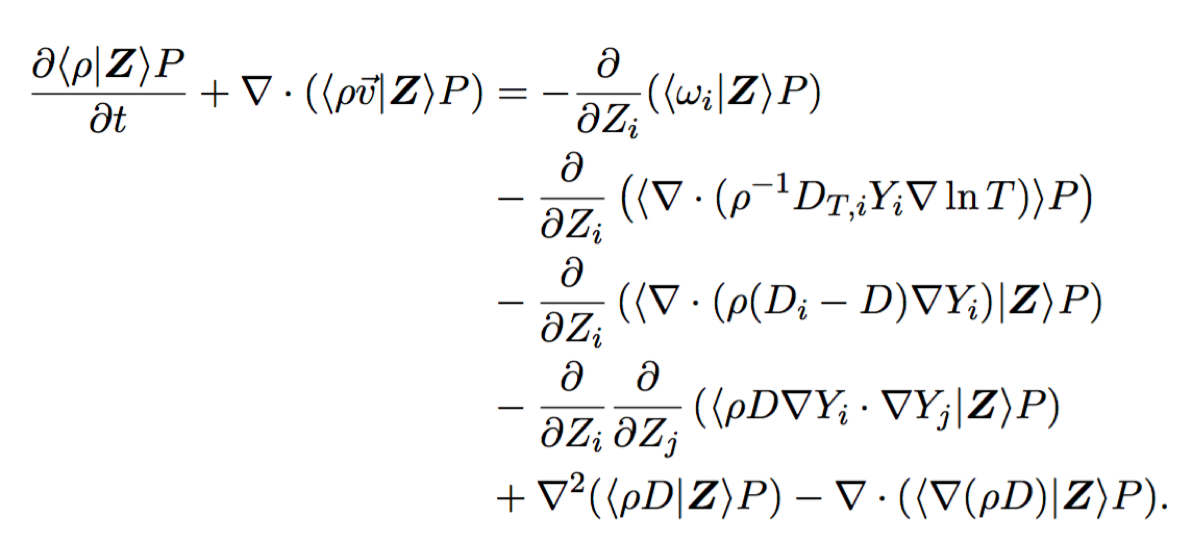
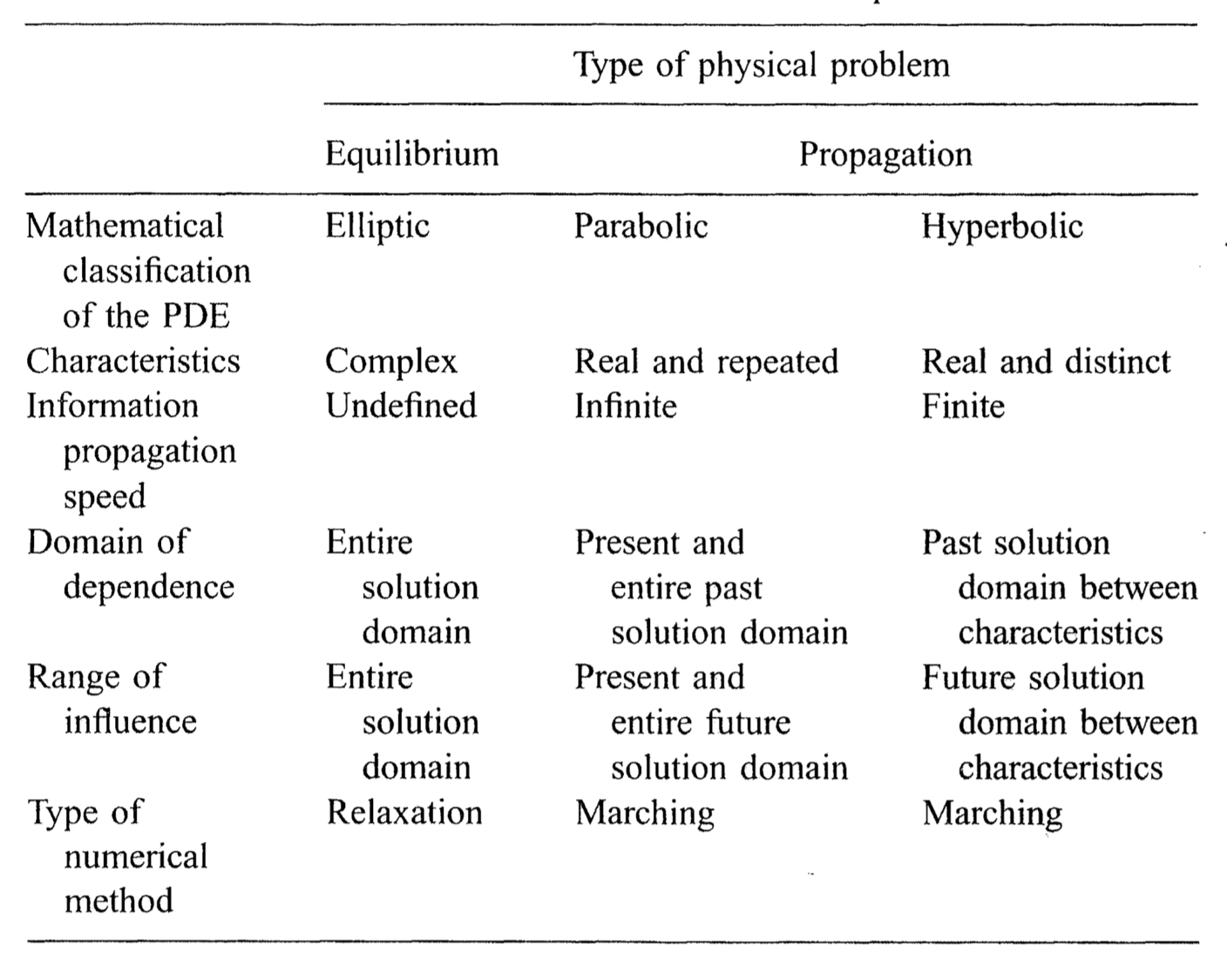
Classification¶
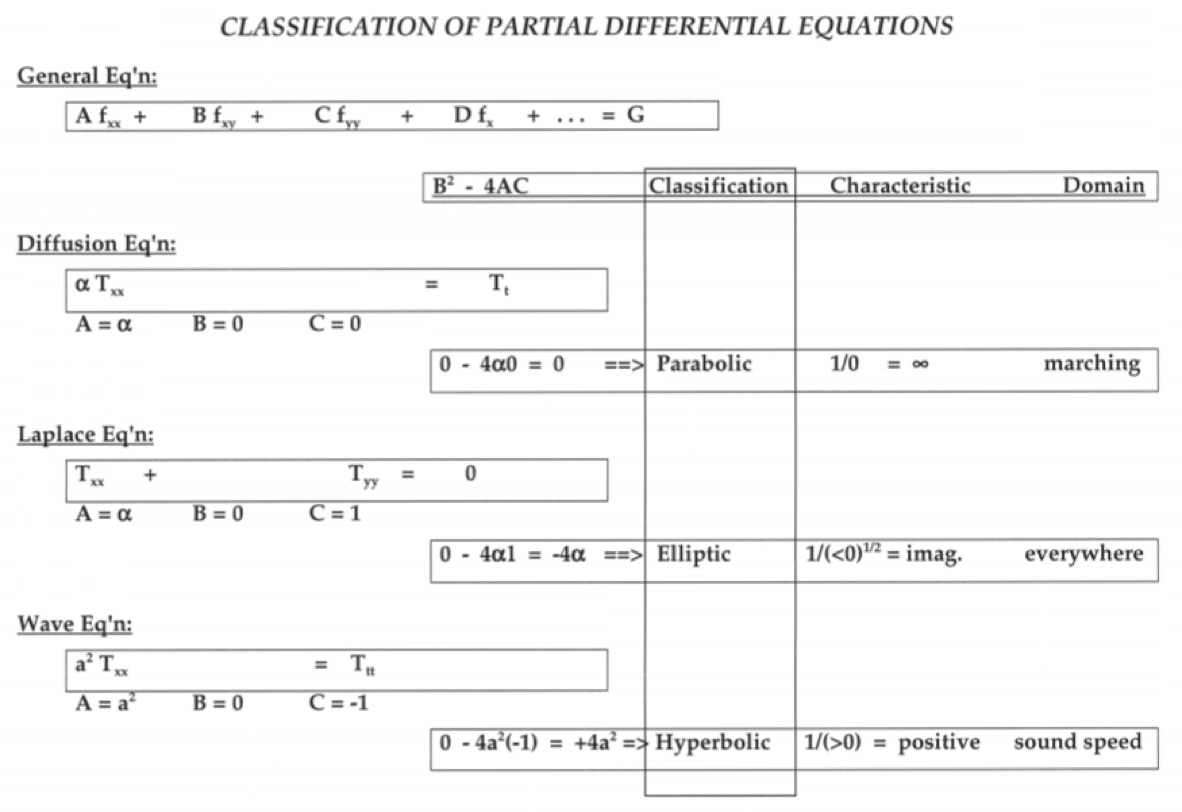
- PDE classification is important as it determines the character of the PDE, hence the types of solution methods we apply to it.
- Quasi-linear PDE (linear in highest derivative):
$$ Af_{xx} + Bf_{xy} + Cf_{yy} + Df_x + Ef_y + Ff = G.$$
- Coefficients $A$, $B$, and $C$ may depend on $x$, $y$, $f_x$, and $f_y$.
- Coefficients $D$, $E$, and $F$ may depend on $x$, $y$, and $f$.
- $G$ may depend on $x$, $y$.
- Note, $x$, $y$, are generic (could be time).
- Discriminant: $B^2 - 4AC$.
- Elliptic: $B^2 - 4AC$ < 0.
- Elliptic problems are diffusive
- Parabolic: $B^2 - 4AC$ = 0.
- Parabolic problems are unsteady diffusive
- Hyperbolic: $B^2 - 4AC$ > 0.
- Hyperbolic problems are convective (wave character).
- Elliptic: $B^2 - 4AC$ < 0.
- Technically, the whole PDE is of one form or another, but often we refer to the character of individual terms in a PDE.
- For example $$\nabla^2\phi + \nabla\cdot(u\phi) = S$$ We would say the first term elliptic, and the second term is hyperbolic.
Domains of dependence¶
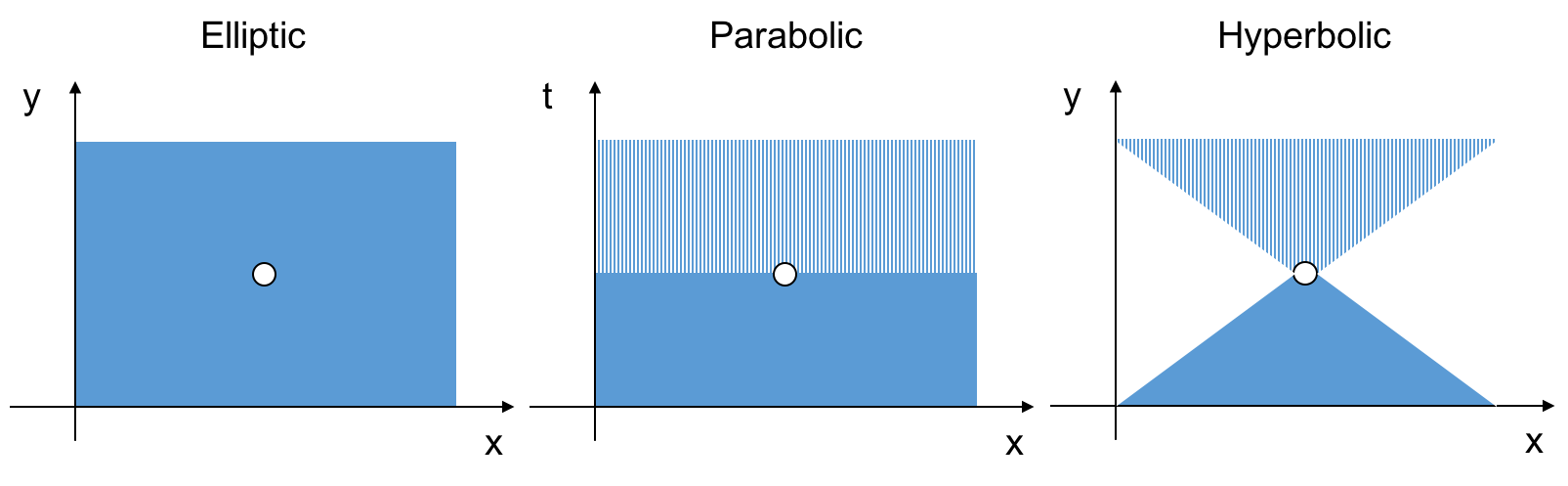
- Elliptic
- Each point depends on every other point in the domain.
- There is no direction of information propagation.
- (Diffusion problems).

- Parabolic
- A given point in the domain depends on every other point spatially, but only depends on past times, not future times.
- Future points depend on past points, but not vice-versa.
- (Marching problems, including unsteady diffusive problems).
- In the figure above, the lower part of the plot is the domain of dependence. The upper part of the plot is the range of influence.

- Hyperbolic
- A given point depends limited regions of the spatial domain.
- This region is defined by characteristic lines (or "characteristics").
- Information propagates along characteristics.
- (Wave propagation, convection).
- Example: 1-D wave propagation:

In [ ]: