PDEs, Stability¶
- FTCS method
- Example
- Von Neumann stability analysis
Example¶
- See Excel example.
- PDE and FTCS method: $$\frac{\partial f}{\partial t} = \alpha\frac{\partial^2f}{\partial x^2},$$ $$f_i^{n+1} = f_i^n + \underbrace{\frac{\alpha\Delta t}{\Delta x^2}}_{d}(f_{i-1}^n-2f_i^n+f_{i+1}^n).$$
- Vary $d$, and examine the results.
- Start with a triangular profile.
- How does the peak decay?
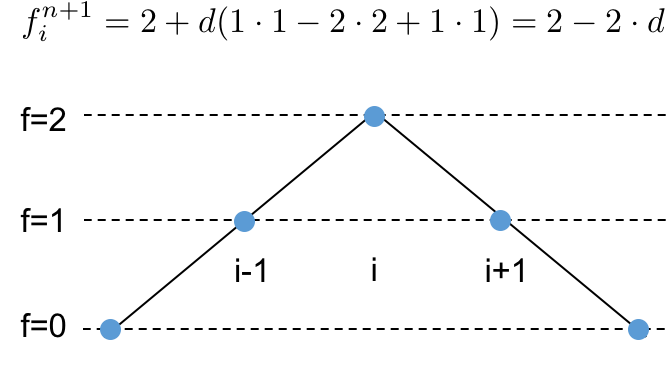
- How does the peak decay?
- Vary the parameter $d$:
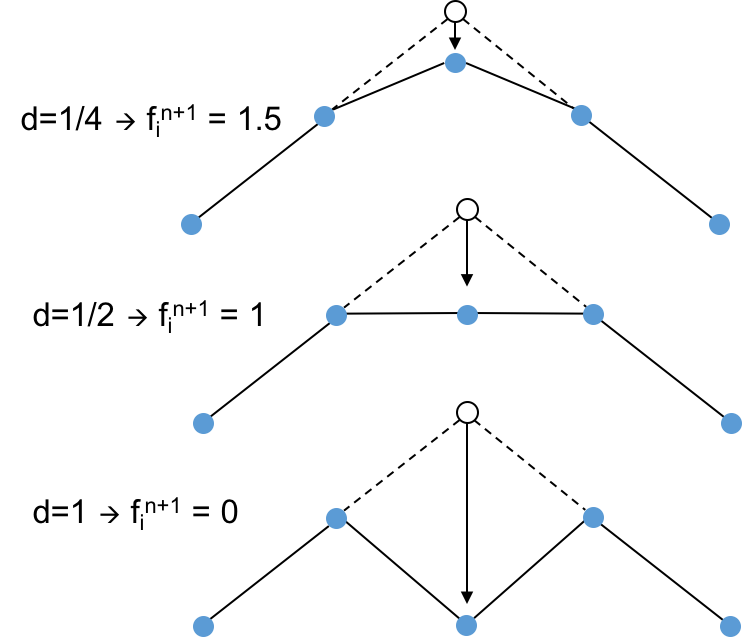
- For even larger $d$, the profile will go negative, which may not even be physical.
- Note, in the PDE:
$$\frac{\partial f}{\partial t} = \alpha\frac{\partial^2f}{\partial x^2} = \alpha\cdot(\mbox{curvature}).$$
- Where there is no curvature, there is no change from one step to the next.
- So, in the above image $f_{i-1}^{n+1} = f_{i-1}^n$, and $f_{i+1}^{n+1} = f_{i+1}^n$. $$f_{i-1}^{n+1} = f_{i-1}^n + d(f_{i-2}^n - 2f_{i-1}^n + f_i^n) = f_{i-1}^n + d(1\cdot 0 - 2\cdot 1 + 1\cdot 2) = f_{i-1}^n + d(0) = f_{i-1}^n.$$
- For large $d$, on the next timestep, the pattern repeates itself on the newly formed twin peaks to continue the oscillatory cycle.
- If $d$ is large enough, the processes is unstable and the oscillations grow in amplitude.
Timescale¶
$$\frac{\partial f}{\partial t} = \alpha\frac{\partial^2f}{\partial x^2},$$
- Nondimensionalize this PDE.
- $f^* = f/f_r \rightarrow f = f^*f_r.$
- $x^* = x/L \rightarrow x = x^*L.$
- $t^* = t/\tau \rightarrow t = t^*\tau.$
- Insert these into the PDE $$\left[\frac{1}{\tau}\right]\left(\frac{\partial f^*}{\partial t^*}\right) = \left[\frac{\alpha}{L^2}\right]\left(\frac{\partial^2 f^*}{\partial x^{*2}}\right).$$
- The units of this equation imply that $$\tau = \frac{L^2}{\alpha}.$$
- This is the characteristic timescale for diffusion.
- If $L=\Delta x$, then $\tau=\Delta x^2/\alpha$.
- Now, we see that our parameter $d$, is a ratio of timescales: $$ d= \frac{\alpha\Delta t}{\Delta x^2} = \frac{\Delta t}{\tau}.$$
- For stability $$d\le \frac{1}{2},$$
- For stability, don't step larger than a factor (1/2) of the characteristic diffusion time across a cell of width $\Delta x$.
- Note how $\Delta t$ is tied to $\Delta x^2$.
- If I use 10$\times$ more grid points, then I have to take 100$\times$ smaller timesteps!
Von Neumann Stability¶
- Here we show that $d\le 1/2$ is the stability criterion.
- Linear PDE with constant coefficients (as above): $$f_t = \alpha f_{xx}.$$
- Express the solution $f(x,t_n)$ as a Fourier Series. $$f(x,t_n) = \sum_{\eta=-\infty}^{\infty}c_{\eta} e^{ik_{\eta}x},$$ $$k_{\eta} = \frac{2\pi\eta}{2L},$$ where $k_{\eta}$ is the wavenumber (inverse wavelength), and $c_{\eta}$ is a complex coefficient.
- The PDE is linear, so we can consider each mode independently,
- e.g., if $f=g+h$ then $f_t=\alpha f_{xx}$ implies $g_t+h_t = \alpha g_{xx}+\alpha h_{xx}.$
- And our above Fourier Series gives $f$ as a sum.
- Now, our FTCS method is
$$f_i^{n+1} = f_i^n + d(f_{i-1}^n-2f_i^n+f_{i+1}^n),$$
- The Fourier Series term implies:
$$f_i = c_{\eta}e^{ik_{\eta}x},$$
$$f_{i+1} = c_{\eta}e^{ik_{\eta}(x+\Delta x)} = \underbrace{c_{\eta}e^{ik_{\eta}x}}_{f_i}e^{ik_{\eta}\Delta x}= f_ie^{ik_{\eta}\Delta x},$$
$$f_{i-1} = c_{\eta}e^{ik_{\eta}(x-\Delta x)} = \underbrace{c_{\eta}e^{ik_{\eta}x}}_{f_i}e^{-ik_{\eta}\Delta x}= f_ie^{-ik_{\eta}\Delta x},$$
- Now, subsitute these into the FTCS equation: $$f_i^{n+1} = f_i^n(1+d(e^{-ik_{\eta}\Delta x} - 2 + e^{ik_{\eta}\Delta x})),$$
- Use $$ e^{ik_{\eta}\Delta x} = \cos(k_{\eta}\Delta x) + i\sin(k_{\eta}\Delta x),$$ to get $$\frac{f_i^{n+1}}{f_i^n} = 1+2d(\cos(k_{\eta}\Delta x)-1) = G,\,\,\mbox{say}.$$
- This will be stable for $|G|\le 1$. This implies
$$-1\le 1 + \underbrace{2d}_{>0}(\underbrace{\cos(k_{\eta}\Delta x)}_{-1\,\mbox{to}\,1}-1) \le 1.$$
- The upper bound in this equation (right-most inequality) is always satisfied.
- For the lower bound, rearranging, we have $$ -2\le2d(\cos(k_{\eta}\Delta x)-1),$$ or $$d\le\frac{1}{1-\cos(k_{\eta}\Delta x)}.$$
- We want the minimum of the right hand side (RHS), since $d$ has to be less than or equal to it. The RHS is minimized for
$$\max(1-\underbrace{\cos(k_{\eta}\Delta x)}_{-1\,\mbox{to}\,1}),$$
- The maximum here is $2$.
- Hence, $$d\le\frac{1}{2}.$$
- This method applies to other PDEs too.
- If the PDE is nonlinear, then linearize it (e.g., Taylor Series), then apply the analysis.
- If the coefficients are not constant, then pretend they are and apply locally.
- Take the most conservative $\Delta t$.
- For example, for $\alpha\Delta t/\Delta x^2\le 1/2$, we have $\Delta t\le (1/2)(\Delta x^2/\alpha)$. Evaluate at $\min(\Delta x^2/\alpha)_i$ on the domain.
In [ ]: