Multidimensional PDEs¶

• Parabolic PDE here: $$\frac{\partial f}{\partial t} = \alpha\frac{\partial^2 f}{\partial x^2} + \alpha\frac{\partial^2 f}{\partial y^2} + S.$$
• Create a two dimensional grid of $(i,\,j)$ points in the $x$ and $y$ directions.
• Take $S$ as constant in time.

FTCS method¶

• Explicit
• $\mathcal{O}(\Delta t),$ $\mathcal{O}(\Delta x^2),$ $\mathcal{O}(\Delta y^2).$

$$f_{i,j}^{n+1} = f_{i,j}^n + \frac{\alpha\Delta t}{\Delta x^2}(f_{i-1,j}^n-2f_{i,j}^n+f_{i+1,j}^n) + \frac{\alpha\Delta t}{\Delta y^2}(f_{i,j-1}^n-2f_{i,j}^n+f_{i,j+1}^n) + \Delta tS_{i,j}.$$

BTCS method¶

• Implicit
• $\mathcal{O}(\Delta t),$ $\mathcal{O}(\Delta x^2),$ $\mathcal{O}(\Delta y^2).$

$$f_{i,j}^{n+1} = f_{i,j}^n + \frac{\alpha\Delta t}{\Delta x^2}(f_{i-1,j}^{n+1}-2f_{i,j}^{n+1}+f_{i+1,j}^{n+1}) + \frac{\alpha\Delta t}{\Delta y^2}(f_{i,j-1}^{n+1}-2f_{i,j}^{n+1}+f_{i,j+1}^{n+1}) + \Delta tS_{i,j}.$$

• Rearrange this equation so that all $n+1$ terms are on the left-hand side (LHS) and all other terms are on the right-hand side (RHS):
• Let $$d_x = \frac{\alpha\Delta t}{\Delta x^2},$$ $$d_y = \frac{\alpha\Delta t}{\Delta y^2}.$$
• Then, $$ (d_y)f_{i,j-1}^{n+1} + (d_x)f_{i-1,j}^{n+1} + (-2d_x-2d_y-1)f_{i,j}^{n+1} + (d_x)f_{i+1,j}^{n+1} + (d_y)f_{i,j+1}^{n+1} = -f_{i,j}^n - \Delta tS_{i,j}. $$

• Or, in coefficient form: $$ (c)f_{i,j-1}^{n+1} + (u)f_{i-1,j}^{n+1} + (a)f_{i,j}^{n+1} + (u)f_{i+1,j}^{n+1} + (c)f_{i,j+1}^{n+1} = b,$$ $$c = d_y,$$ $$u = d_x,$$ $$a = -2d_x-2d_y-1,$$ $$b= -f_{i,j}^n-\Delta tS_{i,j}.$$

• Alternative: if $d_x=d_y$, divide through by by $d_x$. $$ (c)f_{i,j-1}^{n+1} + (u)f_{i-1,j}^{n+1} + (a)f_{i,j}^{n+1} + (u)f_{i+1,j}^{n+1} + (c)f_{i,j+1}^{n+1} = b,$$ $$c = 1,$$ $$u = 1,$$ $$a = -4-\frac{1}{d},$$ $$b= -\frac{f_{i,j}^n}{d}-\frac{\Delta tS_{i,j}}{d}.$$

Matrix form¶

• Our unknowns are on a two-dimensional grid.
• We need to arrange these in one-dimension for solution as a coupled linear system of equations.

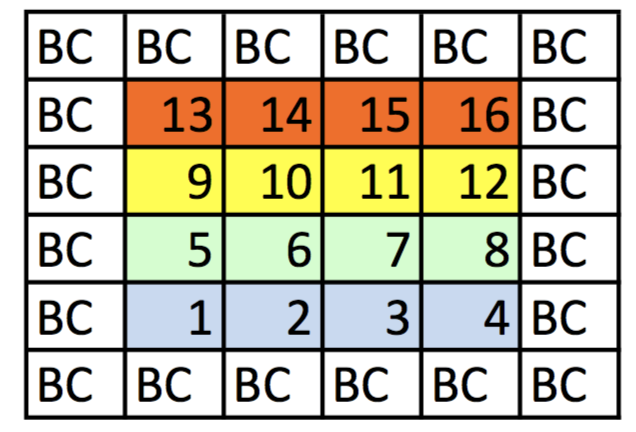
• The points in the grid are numbered sequentially.
• Three types of cells:
  1. Corner
  2. Edge
  3. Interior
• As for 1-D problems, unknown points (cells that are not boundary cells) will refer to neighboring cells.
  • Corner and edge cells will refer to boundary cells due to the discretization stencils of the spatial derivatives in the PDE.
  • These BC point will appear on the RHS of the $Ax=b$ linear system to be solved.
• Considering Dirichlet BCs.

Matrix structure:¶

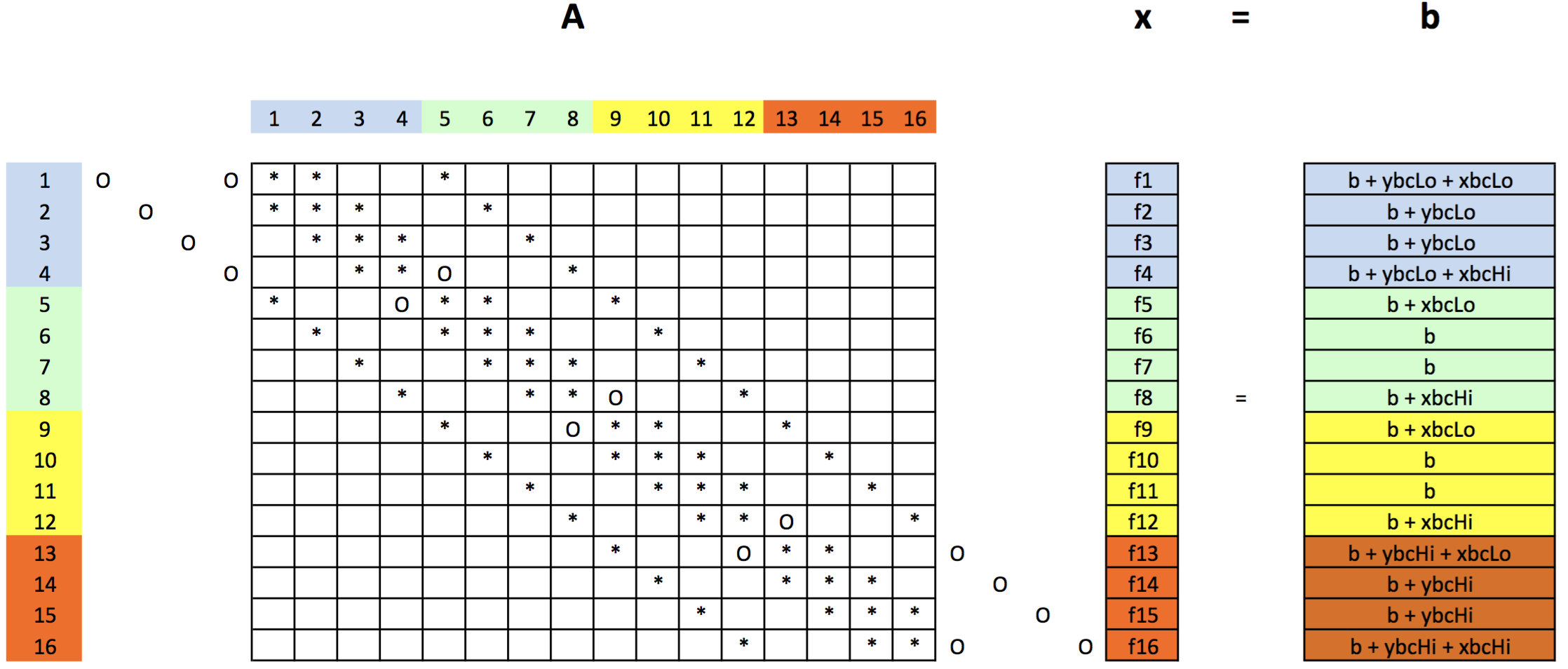
• In the matrix shown, empty cells are zero.
• Note the explicit "O" points where boundary conditons have been moved from the $A$ matrix to the RHS vector $b$.
• Note the explicit "*" points have nonzero values in the matrix.
• Consider grid point 4:
  • It has neighbors: 3 and 8, so in row 4, there are *'s in columns 3, 4, and 8.
  • The "O" in column 5 arises since point 5 is not a neighbor of point 4 and does not appear in point 4's discretization stencil.
  • Instead, point 4's right neighbor is a boundary point, and this boundary augments the 4$^{th}$ element of the $b$ vector. Similarly for the point on the boundary below point 4.

Here is the matrix in terms of coefficients:¶

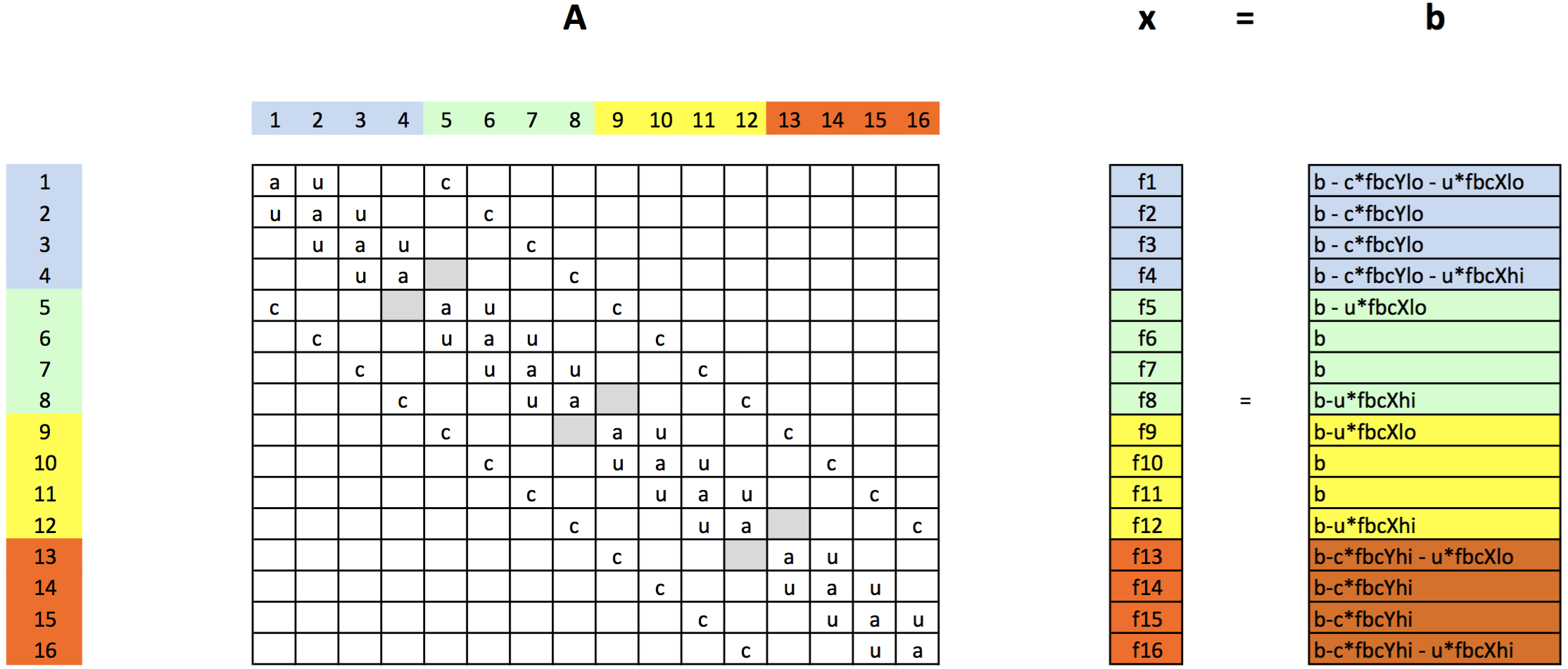
• Note, this is on a grid where the indicies of the unknowns start at 1.
  • Here, point $(i,\,j)$ is unknown number $i+(j-1)\cdot n_x$, where $n_x$ is the number of points in the $x$ direction (4 in the example above).
  • On a grid where the indicies of the unknowns start at 0 (as in Python), we would have point $(i,\,j)$ in the grid corresponds to point $i+j\cdot n_x$ in the list of unknowns.