ODEs: Higher order IVP¶

• EE and IE are simple, but low order: globally first order.
  • To get high accuracy requires many more steps: smaller $\Delta t$.
  • Higher order methods give the same accuracy for larger step sizes.

Second order methods¶

ODE: $$\frac{dy}{dt} = f(y,t),$$ $$y(t=0) = y_0.$$

Modified midpoint (MM) method¶

• EE takes a step from $k$ to $k+1$ using the slope at point $k$.
• IE takes a step from $k$ to $k+1$ using the slope at point $k+1$.
• MM takes a step from $k$ to $k+1$ using the slope at point $k+1/2$.
  • To get to $k+1/2$ so that we can evaluate the slope there, take a trial EE step to that point

$$y_{k+1/2} = y_k + \frac{\Delta t}{2}f(y_k,t_k).$$ $$y_{k+1} = y_k + \Delta tf(y_{k+1/2},t_{k+1/2}).$$

• So, on each step we first evaluate $y_{k+1/2}$ using EE for a half step. Then we take the real full step using the slope at $y_{k+1/2}$.

Taylor series representation¶

• Write two Taylor series approximations for $y_{k+1}$ and $y_k$ centered on $y_{k+1/2}$. $$y_{k+1} = y_{k+1/2} + y^{\prime}_{k+1/2}\frac{\Delta t}{2} + \frac{1}{2}y^{\prime\prime}_{k+1/2}\left(\frac{\Delta t}{2}\right)^2+\frac{1}{6}y^{\prime\prime\prime}_{k+1/2}\left(\frac{\Delta t}{2}\right)^3\ldots,$$ $$y_{k} = y_{k+1/2} - y^{\prime}_{k+1/2}\frac{\Delta t}{2} + \frac{1}{2}y^{\prime\prime}_{k+1/2}\left(\frac{\Delta t}{2}\right)^2-\frac{1}{6}y^{\prime\prime\prime}_{k+1/2}\left(\frac{\Delta t}{2}\right)^3\ldots,$$
• Subtract the second equation from the first and solve for $y_{k+1}$. $$y_{k+1} = y_k + \Delta t y^{\prime}_{k+1/2} + \mathcal{O}(\Delta t^3).$$
• The method is globally $\mathcal{O}(\Delta t^2)$.
• Note, $y^{\prime}_{k+1/2} \equiv f(y_{k+1/2},t_{k+1/2}).$
• Note, this analysis was done using $y_{k+1/2}$, but the actual method doesn't use $y_{k+1/2}$, it uses the EE approximation to this value, so we really have $$y_{k+1} = y_k + \Delta t (y^{\prime}_{k+1/2}+\mathcal{O}(\Delta t^2)) + \mathcal{O}(\Delta t^3),$$ where the $\mathcal{O}(\Delta t^2)$ term is the local error of the EE method. When we expand this we get
  $$y_{k+1} = y_k + \Delta t y^{\prime}_{k+1/2}+\mathcal{O}(\Delta t^3) + \mathcal{O}(\Delta t^3) = y_k + \Delta ty^{\prime}_{k+1/2}+\mathcal{O}(\Delta t^3),$$ so there is no overall change in the global order of the method.

Implicit trapazoid (IT) method¶

• From the MM method: $$ y_{k+1} = y_k + \Delta t y^{\prime}_{k+1/2} = y_k + \Delta t f_{k+1/2}.$$
• Evaluate $$f_{k+1/2} = \frac{1}{2}(f_k + f_{k+1}).$$
• Hence,

$$y_{k+1} = y_k + \Delta t\frac{f(y_k,t_k) + f(y_{k+1},t_{k+1})}{2}.$$

• This method is globally $\mathcal{O}(\Delta t^2)$ accurate.
• Note how and why the method is implicit.
• Note, this method can also be written as EE from $k$ to $k+1/2$ followed by IE from $k+1/2$ to $k+1$: $$y_{k+1/2} = y_k + \frac{\Delta t}{2}f_k,$$ $$y_{k+1} = y_{k+1/2} + \frac{\Delta t}{2}f_{k+1}.$$

Modified Euler (ME) method¶

• This is like the IT method, but get $f_{k+1}$ from a full EE step:

$$ y^*_{k+1} = y_k + \Delta t f_k,$$ $$ y_{k+1} = y_k + \Delta t \frac{f(y_k,t_k) + f(y_{k+1}^*,t_{k+1})}{2}.$$

• This is a two-step predictor-corrector method. We predict the answer using EE in the first step, then using this result, we improve (correct) the answer in the second step.
• This method is globally $\mathcal{O}(\Delta t^2)$ accurate.

Runge Kutta (RK) methods¶

\begin{align*} y_{k+1} = y_k + &hS, \\ & S = c_1S_1 + c_2S_2 + c_3S_3 + \ldots. \end{align*}

• Here, let $h\equiv\Delta t$
• $S$ is a slope $dy/dt$, evaluated from $f(y,t)$ or from a combination of $f(y,t)$ evaluated at various points $y$ in different ways.
  • The $c_i$ above are coefficients of the linear combination.
• Here, we will ignore the time dependence of $f$ for simplicity and clarity.

Second order¶

\begin{align*} y_{k+1} = &y_k + h(c_1S_1 + c_2S_2), \\ &S_1 = f(y_k), \\ &S_2 = f(y_k + \beta hS_1). \end{align*}

• So, we are taking linear combinations of $h$ times the slopes evaluated at different points.
• Note in the second equation we evaluate the slope at a later time. We get to that time by taking an Euler-like step $y_k+\beta hS_1$.
• Combine the above equations:

$$ y_{k+1} = y_k + c_1hf(y_k) + c_2hf(y_k+\beta hS_1).$$

• Again (for slides display):

$$ y_{k+1} = y_k + c_1hf(y_k) + c_2hf(y_k+\beta hS_1).$$

• This equation contains parts at point $k$ and a part at a later time, $f(y_k+\beta hS_1)$.
  • Note that $\beta hS_1 = \beta hf_k$.
• We can write all parts at point $k$ by expanding $f(y_k+\beta hS_1)$ in a Taylor series about point $k$:

\begin{align} f(y_k+\beta\Delta y_1) &= f_k + \left.\frac{\partial f}{\partial y}\right|_k\beta hS_1 + \mathcal{O}(h^2), \\ &= f_k + \beta h f_{y,k} f_k + \mathcal{O}(h^2),\\ \end{align}

where $f_{y,k}$ is the derivative of $f$ with respect to $y$ evaluated at point $k$.

• Hence,

$$ y_{k+1} = y_k + f_k h(c_1+c_2) + \beta h^2c_2f_{y,k}f_k + \mathcal{O}(h^3).$$

• Now, we will take a Taylor series of $y_{k+1}$ and compare it with the above green equation.

  \begin{align} y_{k+1} &= y_k + y_k^{\prime}h + \frac{1}{2} y_k^{\prime\prime}h^2 + \mathcal{O}(h^3),\\ &= y_k + f_kh + \frac{1}{2}h^2(y^{\prime})^{\prime}_k + \mathcal{O}(h^3). \end{align}

  • Now,

  $$(y^{\prime})^{\prime} = \left.\frac{\partial f}{\partial t}\right|_k = \left.\frac{\partial f}{\partial y}\frac{dy}{dt}\right|_k = f_{y,k}f_k.$$

  • Hence:
  $$y_{k+1} = y_k + f_kh + \frac{1}{2}h^2f_{y,k}f_k + \mathcal{O}(h^3).$$

• Again, the green equation above is:

$$ y_{k+1} = y_k + f_k h(c_1+c_2) + \beta h^2c_2f_{y,k}f_k + \mathcal{O}(h^3).$$

• Comparing the green and red equations imples:

$$ (c_1+c_2) = 1, $$ $$\beta c_2 = \frac{1}{2}.$$

• So, in choosing our second order RK method, we have one degree of freedom. Choose, say, $c_1$, then $c_2 = 1-c_1$, and then $\beta = 1/2c_2.$
  • There are an infinite number of possible second order methods.

Example¶

Recall our 2nd order method: \begin{align*} y_{k+1} = &y_k + h(c_1S_1 + c_2S_2), \\ &S_1 = f(y_k), \\ &S_2 = f(y_k + \beta hS_1). \end{align*}

• Let $c_1 = 1/2$, then $c_2=1/2$ and $\beta = 1$. $$y_{k+1} = y_k + \frac{h}{2}(f(y_k) + f(y_k+hf(y_k))$$
• This is the ME method.

Fourth order RK method (The RK method)¶

\begin{align*} y_{k+1} &= y_k + h\left(\frac{1}{6}S_1 + \frac{2}{6}S_2 + \frac{2}{6}S_3 + \frac{1}{6}S_4\right),\\ & S_1 = f(y_k), \\ & S_2 = f(y_k+\frac{h}{2}S_1), \\ & S_3 = f(y_k+\frac{h}{2}S_2), \\ & S_4 = f(y_k+hS_3). \end{align*}

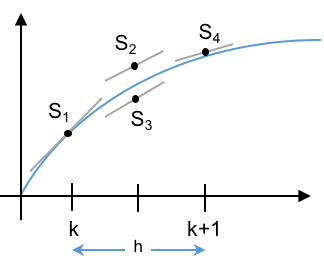
Approach¶

• Evaluate the slope $S_1$ at $y_k$.
• Take a half step EE from point $k$ to $k+1/2$ using slope $S_1$.
  • Evaluate $S_2$ here.
• Take a half step EE from point $k$ to $k+1/2$ using slope $S_2$.
  • Evaluate $S_3$ here.
• Take a full step EE from point $k$ to $k+1$ using slope $S_3$.
  • Evaluate $S_4$ here.
• Take the final full step using a linear combination of the slopes: $$y_{k+1} = y_k + \frac{h}{6}(S_1 + 2S_2 + 2S_3+ S_4).$$
• Note how values of $y$ at intermediate step are used to compute slopes for following steps.
• For $n^{th}$ order with $n\le 4$ $\rightarrow$ $n$ function evaluations are required.
• For $>4^{th}$ order $\rightarrow$ more than $n$ function evaluations required. (Storage costs too).
• $\rightarrow$ the $4^{th}$ order method gives the most bang for the buck.

RK4 code¶

• Solve $dy/dt = -y$ from $t=0$ to $t=5$ with RK4 and EE. Use 10 steps, so $\Delta t = 0.5$. Let $y_0=1$.