Finite volume methods-2

Issues:
- Fluxes with variable properties
  - See S.V. Patankar “Numerical Heat Transfer and Fluid Flow”
- Grid decoupling

Fluxes with variable properties

Consider 1-D, steady state heat conduction on a nonuniform grid. $$q_e-q_w = S\Delta x.$$

$$q_e = -k_e\left(\frac{\partial T}{\partial x}\right)_e,$$ $$q_w = -k_w\left(\frac{\partial T}{\partial x}\right)_w.$$

Consider $q_e$:

$$q_e = -k_e\frac{T_E-T_P}{\delta_e}.$$

We need $k_e$. How to evaluate it?
Try linear interpolation:

$$\frac{k_E-k_e}{\delta_{e+}} = \frac{k_E-k_P}{\delta_e},$$ $$k_e = fk_P + (1-f)k_E,$$ $$f = \frac{\delta_{e+}}{\delta_e}.$$

Unfortunately, this does not work very well.

The finite volume method is still conservative since $q_e$ is applied to the energy balance for both the P and E cells.
- But the solution is not physically accurate when applied to systems with variable properties.

Case 1

Consider the case where cells P and E are different materials.
- Maybe take E as an insulator
- Then $k_E = 0$.
- Expect $q_e = 0$.
- But linear interpolation to evaluate $q_e$ using $k_e$, as shown above, gives the following: $$k_e = \frac{\delta_{e+}}{\delta_e}k_P,$$ $$q_e = -k_e\frac{T_E-T_P}{\delta_e}\ne0.$$
We expect a temperature profile like the following:
Notice that no temperature gradient develops in cell E since it is an insulator. This implies zero heat flux.

Case 2

Now, take a case with $k_E > k_P$.
We expect the following temperature profile (assuming uniform properties throughout a given control volume):
here, $T_I$ is an intermediate temperature at the cell face e.

If we use a uniform temperature gradient throught the region of interest, then consider the heat fluxes that this graph implies

Denote the heat flux on the left and right sides of e as $q_{e-}$ and $q_{e+}$, respectively.

$$q_{e-} = -k_P\frac{T_I-T_P}{\delta_{e-}} = -k_P\frac{T_E-T_P}{\delta e},$$

$$q_{e+} = -k_E\frac{T_E-T_I}{\delta_{e+}} = -k_E\frac{T_E-T_P}{\delta e}.$$

Now, since $k_E\ne k_P$ we have $q_{e-}\ne q_{e+}$.

Hence, using (or implying) the same temperature gradient in both cells (materials) gives different heat fluxes in the two cells when using the respective thermal conductivities.

A linear T profile (same T gradient in both cells) conserves heat flux if the same $k$ is used in both cells.
- That $k$ could be $k_e$ as evaluated by linear interpolation.
- But this gives the unphysical behavior of Case 1.
- And doesn’t imply the physical profile of Case 2.

Solution

Find an evaluation of $k_e$, that is physically consistent with heat fluxes through materials of different properties.

That is, find an evaluation of $k_e$ that allows for different temperature gradients to be implied in cells with different conductivities.

Note, we still want to evaluate the temperature gradient in the usual way, that is $(dT/dx)_e = (T_E-T_P)/\delta_e$.

Construct $k_e$ by equating fluxes in the two cells (so that energy is conserved): * Allow for an intermediate temperature $T_I = T_e$. * Equate the fluxes on the left and right of the interface, and then solve for $T_I$:

$$q_{e-} = q_{e+} \rightarrow -k_P\frac{T_I-T_P}{\delta_{e-}} = -k_E\frac{T_E-T_I}{\delta_{e+}}.$$

$$\rightarrow T_I =\frac{\frac{k_P}{\delta_{e-}}T_P + \frac{k_E}{\delta_{e+}}T_E}{\frac{k_P}{\delta_{e-}} + \frac{k_E}{\delta_{e+}}}$$

Now equate the flux evaluated over both cells P and E (that is, $q_e$), which is written in terms of $k_e$, and equate this to $q_{e-}$.

$$q_e = q_{e-} \rightarrow -k_e\frac{T_E-T_P}{\delta_e} = -k_P\frac{T_I-T_P}{\delta_{e-}}$$

We insert the expression for $T_I$, and then solve for $k_e$:

$$\color{blue}{k_e = \frac{k_Ek_P\delta_e}{k_P\delta_{e+}+k_E\delta_{e-}}.}$$

$$\color{blue}{k_e = \frac{2k_Pk_E}{k_P+k_E},,,,\mathrm{if}, \delta_{e-}=\delta_{e+}.}$$

This is a harmonic mean instead of an arithmetic mean.
Use this for finite volume methods with variable $k$, $\mu$, $D$.
Summary

$$\color{blue}{q_e = -k_e \frac{T_E-T_P}{\delta_e},}$$

$$\color{blue}{k_e = \frac{k_Ek_P\delta_e}{k_P\delta_{e+}+k_E\delta_{e-}}.}$$

Results

Now, for $k_E\rightarrow 0$, $k_e\rightarrow 0$, and $q_e\rightarrow 0$ as it should (unlike the linear interpolation).
For a case with $k_E\gg k_P$ we have $$k_e = \frac{k_P\delta_e}{\delta_{e-}},$$

$$q_e = -\frac{k_P\delta_e}{\delta_{e-}}\frac{T_E-T_P}{\delta_{e}} = -k_P\frac{T_E-T_P}{\delta_{e-}}.$$

This implies that all the change happens in the P cell, with the E cell offering no resistence. Good! This is consistent with the physical situation.

Grid decoupling

There is a problem with first derivatives.
Consider cells W, P, E and a convective flux term where $v$ is velocity and $f$ is some variable.

    |---W---|---P---|---E---|
            w       e

$$\frac{\partial vf}{\partial x}.$$

Integrate this over cell P $$(vf)_e-(vf)_w$$
Then interpolate to find $(vf)_e$ and $(vf)_w$: $$ \frac{v_Ef_E+v_Pf_P}{2} - \frac{v_Pf_P + v_Wf_W}{2},$$ $$ \frac{v_Ef_E-v_Wf_W}{2}.$$
Note how this totally skips the P cell.
If we have a $vf$ field as shown below, the first derivative of $vf$ will be zero everywhere and this profile will persist.

    |---5---|---3---|---5---|---3---|---5---|

This can happen in 2D or 3D:

    |-----|-----|-----|
    |  8  |  3  |  8  |
    |-----|-----|-----|
    |  3  |  5  |  3  |
    |-----|-----|-----|
    |  8  |  3  |  8  |
    |-----|-----|-----|

Or, suppose we take a smooth solution and add a checkerboard pattern (from noise, or errors, etc.), this patter could persist, or even grow.
This happens with pressure P in the fluid equations. The $\nabla P$ term gives $P_e-P_w$ hence $(P_E-P_W)/2$.
- Pressure gradients drive velocity, and we’d like pressure to not skip cells. We don’t want a pressure checkerboard to be preserved or to grow.
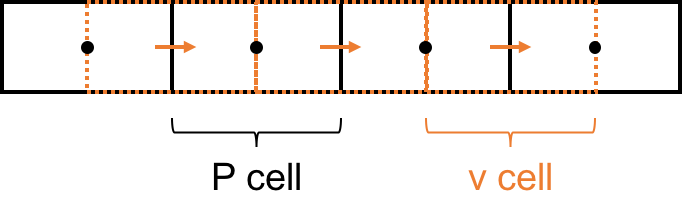
Remedy: Use a staggered grid.
- Velocity is solved on the orange grid cells (v-cells) and
- Pressure is solved on the black grid cells (P-cells).
- When considering the velocity equation we are using the orange grid (v-cells). Then $dP/dx \rightarrow (P_e-P_w)$, but these values are known directly on the black grid (P-cells) and no interpolation is necessary, and no checkerboarding occurs.

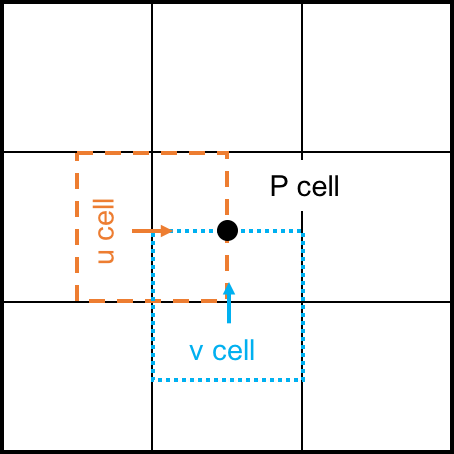
In 2-D, we have P-cells in the center, u-cells shifted to the left, and v-cells shifted down.
Normally, scalars such as pressure, temperature, species mass fractions, etc. are evaluated using P-cells, and velocity vectors are on u-cells, v-cells, and w-cells.
This is convenient for discretization, and numerically very stable.

Grids are called either staggered or collocated.