ADI method, Elliptic, Parabolic PDEs

Previously, the two dimensional, implicit parabolic PDE resulted in a penta-diagonal system of equations to solve at each point in time.
A canonical elliptic equation is like a steady version of the parabolic equation:

$$\alpha\frac{\partial^2f}{\partial x^2} + \alpha\frac{\partial^2f}{\partial y^2} + S(x,y) = 0.$$

Again, we define a two-dimensional grid and apply centered difference approximations to the derivatives.

$$\frac{\alpha}{\Delta x^2}(f_{i-1,j} - 2f_{i,j} + f_{i+1,j}) + \frac{\alpha}{\Delta y^2}(f_{i,j-1} - 2f_{i,j} + f_{i,j+1}) + S_{i,j} = 0.$$

This is written in coefficient form as

$$uf_{i,j-1} + cf_{i-1,j} + af_{i,j} + cf_{i+1,j} + uf_{i,j+1} = b_{i,j}.$$

When ordering the grid sequentially from left to right and top to bottom we obtain a penta-diagonal system of linear equations to solve.

Linear solution

Direct methods:
- This system could be solved with a purpose-built direct solver like an extention of the Thomas Algorithm.
Iterative methods:
- More common
- Start with an initial guess of the solution, and iterate to convergence.
- Jacobi, Gauss-Seidel, SOR
- Conjugate Gradient method
- Multigrid methods
- Alternating direction implicit (ADI) method.

The Thomas Algorithm was fast and easy to implement.
ADI is an iterative method, not unlike Gauss-Seidel, that arranges the unknowns in such a way that the system is tridagonal at each iteration step.
There are two approaches

Order the grid in two ways (A), and (B) (boundary points not shown):
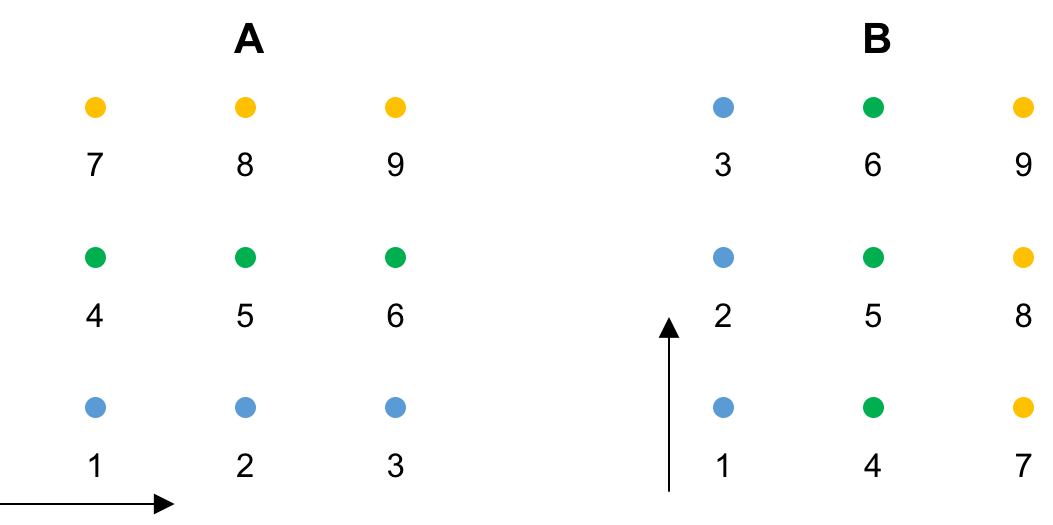
These 3x3 grids (9 unknowns) will result in 9x9 matrices.
Grid (A), for any given point, the top and bottom neighbors are on diagonals $\pm n_x$
- Tridaigonal with $\pm j$ on off-diagonals $\pm n_x$
- In each equation move $y$-directed neighbors to the RHS of the equation and use previous values to evaluate them.
Grid (B), for any given point, the left and right neighbors are on diagonals $\pm n_y$.
- Tridaigonal with $\pm i$ on off-diagonals $\pm n_y$.
- In each equation move $x$-directed neighbors to the RHS of the equation and use previous values to evaluate them.

Alternate the grids. Each iteration solves Grid (A) then Grid (B). Iterate to convergence.

Instead of considering the whole 9x9 system, we treat the 2-D grid as a sequence of 1-D problems.
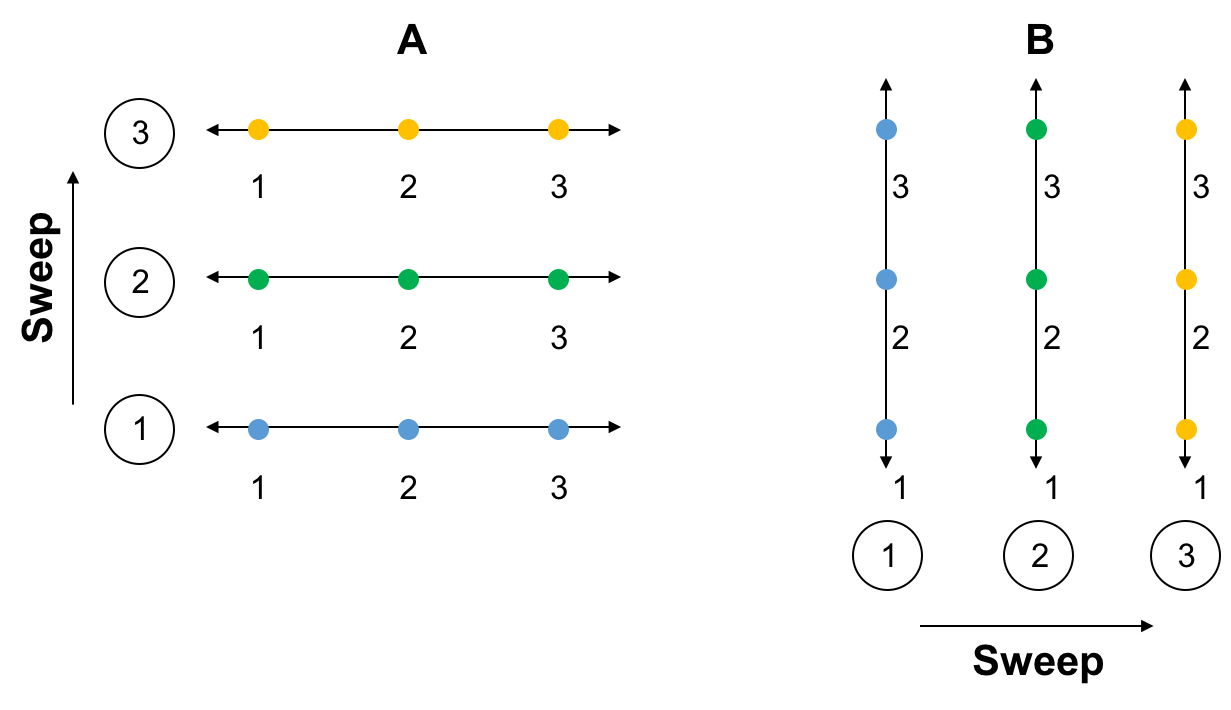
- We sweep the grid in the y-direction, then the x-direction.
Grid A
- For line (1), we form a tridiagonal system with points (1), (2), and (3) as the unknowns.
  - That is, points $f_{1,1}$, $f_{1,2}$, $f_{1,3}$ are the unknowns.
  - All other points in the 2-D, 5-point stencil are considered known.
  - This gives a 3x3 tridiagonal matrix for the grid shown.
  - We solve this system and update the three points.
- Repeat this for line (2), then line (3).
- Note that we are coupling the x-direction points and decoupling the y-direction points.
Grid B
- Follow the same approach as in Grid A.
- But now, we are coupling the y-direction points and decoupling the x-direction points.
One iteration consists of sweeping lines (1), (2), and (3) on Grid A, followed by sweeping lines (1), (2), and (3) on Grid B.
Matricies are setup in the usual fashion, with decoupled points on the RHS, and boundary conditions properly specified.

ADI 1 is more matrix-centric
ADI 2 is more grid-centric
Note how these ADI methods fully couple one dimension at a time allowing full information propagation in the given direction.
The pentadiagonal solve only requires one iteration.
The Gauss-Seidel method decouples both directions, so information propagates more slowly across the domain.
The ADI is in-between.
In 3-D we have a heptadiagonal system with three grids.
- For ADI 1, we again move four of the seven off diagonals to the RHS, and alternate between the grid ordering.
- For ADI 2, we sweep lines in the x, y, and z directions sequentially.
Elliptic methods are very common, but often occur as parts of larger problems.
- In fluid mechanics, the pressure Poisson equation is an example.
All of this applies to implicit parabolic problems such as the BTCS and CN methods.

For parabolic problems, Hoffman gives an ADI alternative.
- Rather than converge the ADI algorithm at each timestep, (since we have a $\Delta t$ truncation error anyway), we can solve as follows:
$$\frac{{f_{i,j}^{n+1}}-f_{i,j}^n}{\Delta t} = \alpha{\left(\frac{\partial^2f}{\partial x^2}\right)_{i,j}^{n+1} + } \alpha\left(\frac{\partial^2f}{\partial y^2}\right)_{i,j}^n + S_{i,j}^n,$$$$\frac{{f_{i,j}^{n+2}}-f_{i,j}^{n+1}}{\Delta t} = \alpha\left(\frac{\partial^2f}{\partial x^2}\right)_{i,j}^{n+1} + \alpha{\left(\frac{\partial^2f}{\partial y^2}\right)_{i,j}^{n+2}} + S_{i,j}^{n+1}.$$
- On one timestep we implicitly couple the x-direction and the y-direction is decoupled (explicit).
- On the next timestep, we implicitly couple the y-direction and the x-direction is decoupled (explicit).