Mass transfer¶

• Combustion involves many chemical species.
• A rigorous treatment of mass transfer is often important.

Velocity¶

• If we could see a molecular view of a flow, we would not see a "velocity," we would see many molecules, each with their own velocity.
• If we consider the average velocity of a particular species, we can define average velocities
  • Mass average
  • Mole average
  • Volume average

Mass and mole flux¶

• Total mass flux for a mass average velocity $$\dot{m}^{\prime\prime} = \rho v$$
• Species $A$ $$\dot{m}^{\prime\prime}_A = \rho y_A v_A$$
• Total molar flux for a molar average velocity $$\dot{n}^{\prime\prime} = c v$$
• Species $A$ $$\dot{n}^{\prime\prime}_A = c x_A v_A$$

Diffusion velocity¶

$$v_A = v_A + v-v$$ $$v_A = v + \underbrace{(v_A - v)}_{v_A^{D}}$$

• Mass flux $$\dot{m}^{\prime\prime}_A = \rho y_Av_A = \rho y_Av + \rho y_Av_A^{D}$$

$$\dot{m}^{\prime\prime}_A = y_A\dot{m}^{\prime\prime} + j_A$$

• This last expression is (Bulk flux of A) + (Diffusion flux of A)
• $j_A$ is the diffusion flux.
• Now, add all species: $$\dot{m}^{\prime\prime} = \sum_i\dot{m}^{\prime\prime}_i = \sum_iy_i\dot{m}^{\prime\prime}+\sum_ij_i = \dot{m}^{\prime\prime}\sum_iy_i + \sum_ij_i = \dot{m}^{\prime\prime} + \sum_ij_i $$

$$\rightarrow \sum_ij_i = 0$$

• The diffusion flux is a difference from an average flux. So, the sum of all diffusion fluxes should be zero.

Multicomponent mass transfer¶

• Model the $j_i$ as gradients of species.
• Using a mole basis is more physical.
• $J_i$ is the molar flux of species $i$
• Fluxes depend on mole fraction gradients.

Two species 1, 2¶

$$J_1 = -cD\nabla x_1,$$ $$J_2 = -cD\nabla x_2.$$

Three species 1, 2, 3¶

$$J_1 = -cD_{1,1}\nabla x_1 - cD_{1,2}\nabla x_2,$$ $$J_2 = -cD_{2,1}\nabla x_1 - cD_{2,2}\nabla x_2.$$

• The flux of one species depends on its own gradient and on the gradient of other species.
  • Other species can drag on each other.
  • Species can diffuse up their gradients!
• Question why do we not include $\nabla x_3$ in $J_1$ above?

Matrix form¶

$$\mathbf{J} = -c[D]\mathbf{\nabla x},\phantom{xxxxxx}\text{size = }n_s-1$$

• $[D]$ is a diffusion matrix defined as follows

$$[D] = [B]^{-1}$$

$$B_{i,j} = -x_i\left(\frac{1}{\mathcal{D}_{i,j}} - \frac{1}{\mathcal{D}_{i,n_s}}\right),\phantom{xxx} i\ne j$$

$$B_{i,i} = \frac{x_i}{\mathcal{D}_{i,n}} + \sum_{k=1,i\ne k}^{n_s} \frac{x_k}{\mathcal{D}_{i,k}}$$

• $\mathcal{D}_{i,j}$ are binary diffusion coefficients.
  • Available in tables. See Turns Appendix D.
  • Cantera can provide these also.
  • $\mathcal{D}_{i,j} \propto T^{3/2}/P$

Fick's law¶

• Beware, there are various forms of "Fick's" law.
• We will use the "best" one

$$J_i = -cD_{i,e}\nabla x_i$$

• $D_{i,e}$ is an effective diffusivity
• To get mass flux, multiply by $M_i$

$$j_i = M_iJ_i = -M_icD_{i,e}\nabla x_i$$

• Use $c=\rho/M$, and $x_i = y_iM/M_i$

$$ j_i = -\frac{M_i\rho}{M}D_{i,e}\frac{M}{M_i}\nabla y_i - \frac{M_i\rho}{M}D_{i,e}\frac{y_i}{M_i}\nabla M$$

$$j_i = -\rho D_{i,e}\nabla y_i - \left(\rho D_{i,e}y_i\frac{\nabla M}{M}\right)$$

• The second term, in parentheses is often ignored.
  • Not a great assumption for combustion.
  • Often used in combustion models for turbulent flow.

Note: $J_i$ is relative to a molar average velocity. So, our conversion to $j_i$ and the use of a mass average velocity is not fully consistent.

Note: In combustion, we often have lots of $N_2$ and using Fick's law instead of a full multicomponent treatment is not that bad.

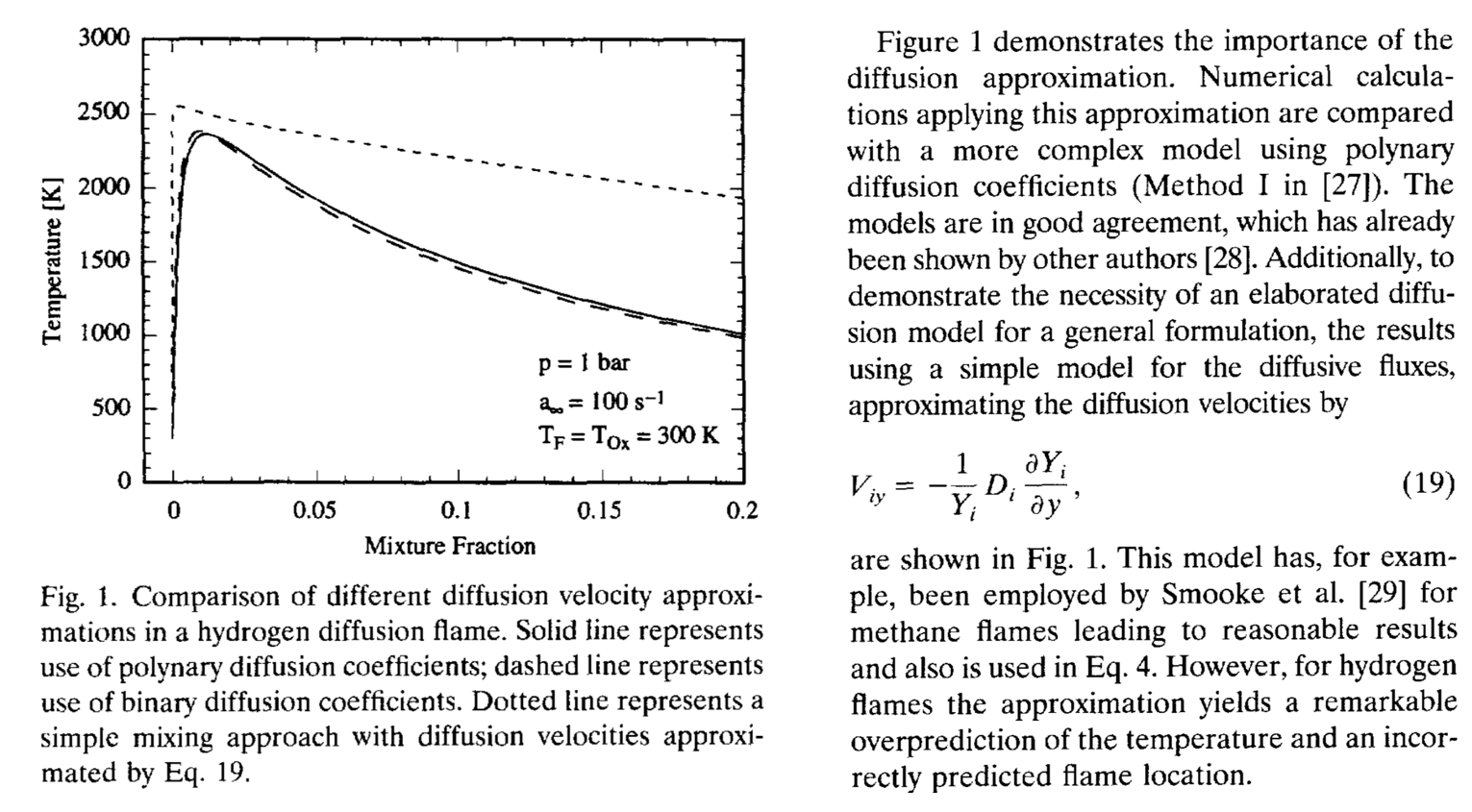
$$D_{i,e} = \left[\frac{(1-x_i)}{\sum_{j=1,j\ne i}^n \frac{x_j}{\mathcal{D}_{i,j}}}\right]$$

The following illustrates the importance of using the "full" Fick's law form given above. This is from Pitsch and Peters (1998).

Heat, Mass, Momentum¶

• Mass transfer: $$\rho y_i \rightarrow j_i = -\rho D\nabla y_i$$
• Heat transfer: $$\rho h \rightarrow q = -\lambda \nabla T$$
• Momentum transfer: $$\rho u \rightarrow \tau = -\mu \nabla v$$

Also, $$ y_i \rightarrow -D\nabla y_i$$ $$ T \rightarrow -\alpha\nabla T$$ $$ v \rightarrow -\nu\nabla v$$

• $\alpha = \lambda/(\rho c_p)$

• $\nu = \mu/\rho$

• $D$, $\alpha$, $\nu$ all have units of $m/s^2$

• For constant properties, the unsteady diffusion equation for some scalar $\eta$, with diffusivity $\Gamma$ is $$\frac{\partial \eta}{\partial t} = \Gamma \frac{\partial^2\eta}{\partial x^2}$$

Dimensionless numbers¶

• Lewis number $$ Le = \frac{\alpha}{D}$$
• Schmidt number $$ Sc = \frac{\nu}{D}$$
• Pr number $$ Pr = \frac{\nu}{\alpha}$$

One-dimensional species transport equation¶

$$\frac{\partial \rho y_i}{\partial t} + \frac{\partial}{\partial x}(\rho y_i v_i) = S_i$$

$$v_i = v + v_i^D$$ $$\rho y_i v_i^D = j_i$$

$$\frac{\partial \rho y_i}{\partial t} + \frac{\partial}{\partial x}(\rho y_i v) + \frac{\partial j_i}{\partial x} = S_i$$