Equilibrium by Gibbs minimization¶

Equilibrium criteria is¶

$$(dG)_{T,P}=0$$

$$G = G(T,P,n_i)$$

$$dG = \frac{\partial G}{\partial T}dT + \frac{\partial G}{\partial P}dP + \sum_i\frac{\partial G}{\partial n_i}dn_i$$

$$(dG)_{T,P}= \sum_i\frac{\partial G}{\partial n_i}dn_i$$

• Here, we have $N_s$ species, with a given species denoted by index $i$.

• Assume from now on that we have constant $T$ and $P$ and drop the $T,P$ subscripts that explicitly indicate constant $T$ and $P$.

• Note the following equivalences

$$dG = \sum_i\frac{\partial G}{\partial n_i}dn_i = \sum_i\mu_idn_i = \nabla G\cdot\mathbf{dn}$$

• $\nabla$ is the gradient in the $n_i$ space.

• Now, $\mathbf{dn}$ is arbitrary, so, for $dG=0$, we have $\nabla G=0$. That is, we are minimizing $G$ in the $n_i$ space.

• At constant $T$, we can divide by $RT$ and bring inside the $\nabla$.

$$\nabla\frac{G}{RT} = 0$$

$$\sum_i\frac{\mu_i}{RT} = 0$$

• Define $\mu_i/RT$ in terms of species moles $n_i$ and total moles $n_t = \sum_i n_i$

$$ \begin{align*} \frac{\mu_i}{RT}&= \frac{g_{i,f}^o}{RT} + \ln\left(\frac{P_i}{P^o}\right), \\ &= \underbrace{\frac{g_{i,f}^o}{RT} + \ln\left(\frac{P}{P^o}\right)}_{\hat{g}_i} + \ln\left(\frac{n_i}{n_t}\right). \end{align*} $$

$$\frac{\mu_i}{RT} = \hat{g}_i + \ln\left(\frac{n_i}{n_t}\right)$$

• Summary: for equilibrium, solve the following for species moles $n_i$

$$\nabla\frac{G}{RT} = \sum_i\left[\hat{g}_i + \ln\left(\frac{n_i}{n_t}\right)\right]\mathbf{e_i} = 0,\phantom{xxx} i=1,\,N_s$$ Here, $\mathbf{e_i}$ is a unit vector in the species $i$ direction.

Elemental constraints¶

• We can't have just any $n_i$.
• We need $n_i$ that conserve elements: $C$, $H$, $O$, $N$, etc.
  • denote elements with index $k$.
  • For some initial mixture (reactants), we find the equilibrium composition, subject to the constraints that elements are conserved.
• $A_k$ total moles of element $k$
• $a_{i,k}$ is the moles of element $k$ is species $i$
• $N_e$ is the number of elements.

$$A_k = \sum_i n_ia_{i,k},\phantom{xxx} k=1,\,N_e$$

• Constraint functions: $$c_k(n_i) = \sum_in_ia_{i,k} -A_k= 0$$

• How do we minimize $G$, AND satisfy the elemental constraints?

Lagrange multipliers¶

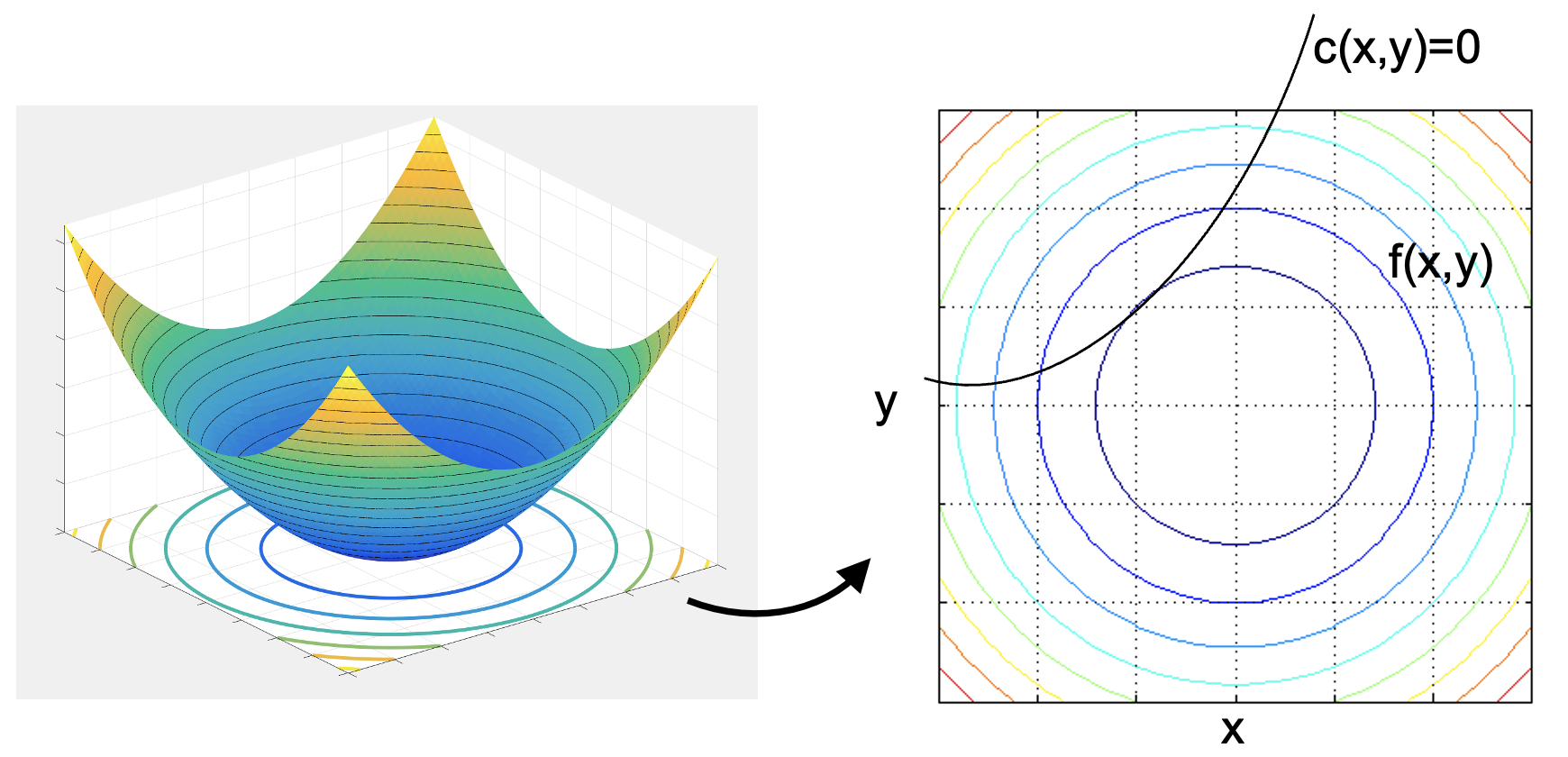
• Minimize a function $f(x,y)$ subject to constraint $c(x,y)=0$
• At the mimimum $\nabla f = 0$
• In the picture shown, $f(x,y)$ has a minimim in the center of the contours.
• But subject to the constraint of being on curve $c(x,y)=0$, we want the miminimum of $f(x,y)$ along that curve.
• This occurs when the isocontours of $f(x,y)$ are tangent to $c(x,y)=0$.
  • That is, the point where contours of $f(x,y)$ are tangent to $c(x,y)=0$.
• The tangent criteria is when $\nabla f$ and $\nabla c$ are in a line
  • Note that $c(x,y)=0$ is our constraint line, but we could have a surface $z=c(x,y)$ and we consider the corresponding $\nabla c$. Our constraint puts us on the particular contour of $z=0$ of the $c(x,y)$ surface. $$\nabla f - \lambda \nabla c = 0$$
  • Or, $\nabla f = \lambda \nabla c$, where $\lambda$ is some scalar variable.
  • Vector $\nabla f$ minus a multiple $\lambda$ of vector $\nabla c$ cancel. This only happens when the two vectors are parallel.
• Our point is then defined by $\nabla f - \lambda \nabla c = 0$, and $c(x,y)=0$, or $$\frac{\partial f}{\partial x} - \lambda \frac{\partial c}{\partial x} = 0,$$ $$\frac{\partial f}{\partial y} - \lambda \frac{\partial c}{\partial y} = 0,$$ $$c(x,y) = 0$$
  • This is 3 equations in 3 unknowns: $x$, $y$, and $\lambda$

More dimensions and constraints¶

• Now, the above was 2D with 1 constraint
• For 3D with 1 constraint
  • The $f(x,y,z)$ isocontour is tangent to the $c(x,y,z)=0$ line.
• For 3D with 2 constraints
  • $c_1(x,y,z)=0$, $c_2(x,y,z)=0$
  • $f(x,y,z)$ is not necessarily tangent to $c_1$ or $c_2$, but it is tangent to the line of intersection of surfaces $c_1$ and $c_2$
  • In 3D $c_1=0$ and $c_2=0$ will be surfaces. When both are satisfied, we will be on the line of intersection of these two surfaces. $f$ is then minimum along this line when contours of $f$ are tangent to this line of intersection. $$\nabla f - \lambda_1\nabla c_1 - \lambda_2\nabla c_2 = 0$$
• In general, we will have at least one fewer constraint than the number of dimensions.
• If we have $k$ constraints, then $$\nabla f - \sum_k\lambda_k\nabla c_k=0$$

Equilibrium¶

For equilibrium $f\equiv G/RT$, and $c\equiv c_k$, given above. Hence, $$\nabla\frac{G}{RT} - \sum_k\lambda_k\nabla c_k= 0.$$

• The gradient operators each have $N_s$ additive terms, one for each species. For the whole equation to be 0, each term will be zero. This gives $$\hat{g}_i + \ln\left(\frac{n_i}{n_t}\right) - \sum_k\lambda_ka_{i,k}=0,\phantom{xxxx}i=1,\,N_s$$ Along with the constraint equations $$\sum_in_ia_{i,k}=A_k, \phantom{xxx}k=1,N_e,$$ and the normalization condition $$n_t=\sum_in_i.$$

• Divide the second and third equations through by $n_t$, and solve the first equation for $x_i=n_i/n_t$:

$$x_i = \exp\left(-\hat{g}_i + \sum_ka_{i,k}\lambda_k\right), \phantom{xxx} i=1,N_s\tag{1}$$

$$\sum_ix_ia_{i,k} = A_k/n_t, \phantom{xxx} k=1,N_e\tag{2}$$

$$\sum_ix_i = 1.\tag{3}$$

• We have $N_s+N_e+1$ equations in unknowns $x_i$, $\lambda_k$ and $n_t$

Reduce equations¶

• We can easily have thousands of species. This would require solving thousands of coupled nonlinear equations.
• Simplify by inserting Eq. (1) above into Eqs. (2) and (3):

$$\sum_ia_{i,k}\exp\left(-\hat{g}_i + \sum_{j}\lambda_j a_{i,j}\right) = A_k/n_t,\phantom{xxxx} k=1,\,N_e$$ $$\sum_i\exp\left(-\hat{g}_i + \sum_k\lambda_ka_{i,k}\right) = 1$$

• note in the equation above we have a sum over $j$ since index $k$ is already used.
• These are a set of $N_e+1$ equations in unknowns $\lambda_k$, $n_t$.

Matrix form¶

• The above equations can be written in a matrix form.

$$\mathbf{[a]}^{T}\exp(-\mathbf{\hat{g}}+\mathbf{[a]}\boldsymbol{\lambda}) = \mathbf{A}/n_t,$$ $$\sum_i\exp(-\mathbf{\hat{g}}+\mathbf{[a]}\boldsymbol{\lambda}) = 1.$$ $$\mathbf{x} = \exp(-\mathbf{\hat{g}} + \mathbf{[a]}\boldsymbol{\lambda})$$

• $\mathbf{A}$, and $\boldsymbol{\lambda}$ are vectors of length $N_e$, and $\mathbf{\hat{g}}$, $\mathbf{x}$ are vectors of length $N_s$; $\mathbf{[a]}$ is the $N_s\times N_e$ matrix of elemental compositions of the species.
• For the species $CH_4, CO_2, CO, H_2O, N_2, H_2$, we have $\mathbf{[a]} = $

	C	H	O	N
$CH_4$	1	4	0	0
$CO_2$	1	0	2	0
$CO$	1	0	1	0
$H_2O$	0	2	1	0
$N_2$	0	0	0	2
$H_2$	0	2	0	0

• We solve the first two blue equations for $\boldsymbol{\lambda}$ and $n_t$. Then we solve the green equation for the species vector $\mathbf{x}$.

Element potentials¶

Consider the green equation $$\mathbf{x} = \exp(-\mathbf{\hat{g}} + \mathbf{[a]}\boldsymbol{\lambda})$$

We can rearrange this to $$\mathbf{[a]}\boldsymbol{\lambda} = \mathbf{\hat{g}} + \ln(x) = \boldsymbol{\mu}/RT $$

The first and last parts are $$\mathbf{[a]}\boldsymbol{\lambda} = \boldsymbol{\mu}/RT $$

Chemical potentials $\mu_i$ are linear combinations of element potentials $\lambda_k$. $$\sum_k\lambda_ka_{i,k} = \mu_i/RT$$

Solution approach¶

• Solve the above two blue equations for $\lambda_k$ and $n_t$.

  • Use Newton's method.

• Then, solve for species composition $x_i$ using the green equation above.

• This approach can be used at a given $T$ and $P$. If enthalpy is known instead of $T$, then we can either add an enthalpy equation like $H = H(T,n_i)$, or we can guess temperature solve equilibrium, and then do an iteration on this process to find T that satisfies $H=H(T,x_i)$.

• We need an initial guess for the $\lambda_k$.

  • If we guess $\mathbf{x}$, then we can invert the green equation to find $\lambda$. But there are more $x_i$ than $\lambda_k$. That is, there are more constraints than degrees of freedom, so we use linear least squares.
    • For generic $Ax=b$, where the length of $b$ is greater than the length of $x$ (and $A$ is rectangular), the linear least squares solution is $A^TAx = A^Tb$. We solve this for $x$ given $b$.
    • For our problem, we have $[a]^T[a](\lambda) = [a]^T(\hat{g}+\ln(x))$.

Solver¶

• Use Cantera for thermochemical properties
• You will need streams.py.
  • This has greek letters in the text, so right click and save as, don't copy and paste text from the browser.
• You also need to have cantera installed. See this link.

Analytic Jacobian¶

Nonlinear solvers based on Newton's method use the Jacobian matrix. This can be computed numerically, but when an analytical Jacobian is available it is best to use it.

Write our equations as $f$ and $h$:

$$f_k = \sum_ia_{i,k}\exp\left(-\hat{g}_i + \sum_{j}\lambda_j a_{i,j}\right) -A_k/n_t= 0,\phantom{xxxx} k=1,\,N_e$$ $$h = \sum_i\exp\left(-\hat{g}_i + \sum_k\lambda_ka_{i,k}\right) -1 = 0$$

The Jacobian matrix is then $$J = \begin{pmatrix} \frac{\partial f_1}{\partial \lambda_1} & \ldots & \frac{\partial f_1}{\partial \lambda_{N_e}} & \frac{\partial f_1}{\partial n_t} & \\ \vdots & \ldots & \vdots & \vdots \\ \\ \frac{\partial f_{N_e}}{\partial \lambda_1} & \ldots & \frac{\partial f_{N_e}}{\partial \lambda_{N_e}} & \frac{\partial f_{N_e}}{\partial n_t} & \\ \frac{\partial h}{\partial \lambda_1} & \ldots & \frac{\partial h}{\partial \lambda_{N_e}} & \frac{\partial h}{\partial n_t} \end{pmatrix}$$

The four main components are given by

$$\begin{align} &\frac{\partial f_k}{\partial\lambda_m} = \sum_ia_{i,k}\exp\left(-\hat{g}_i+\sum_ja_{i,j}\lambda_j\right)a_{i,m}, \\ &\frac{\partial f_k}{\partial n_t } = A_k/n_t^2, \\ &\frac{\partial h}{\partial \lambda_m} = \sum_i\exp\left(-\hat{g}_i+\sum_ka_{i,k}\lambda_k\right)a_{i,m}, \\ &\frac{\partial h}{\partial n_t} = 0. \end{align}$$