Engines and fuels¶
Otto cycle¶
- Gasoline engines
- 4-stroke cycle
- Intake
- Compression
- Combustion at the top
- Expansion/power
- Exhaust
Idealized cycle¶
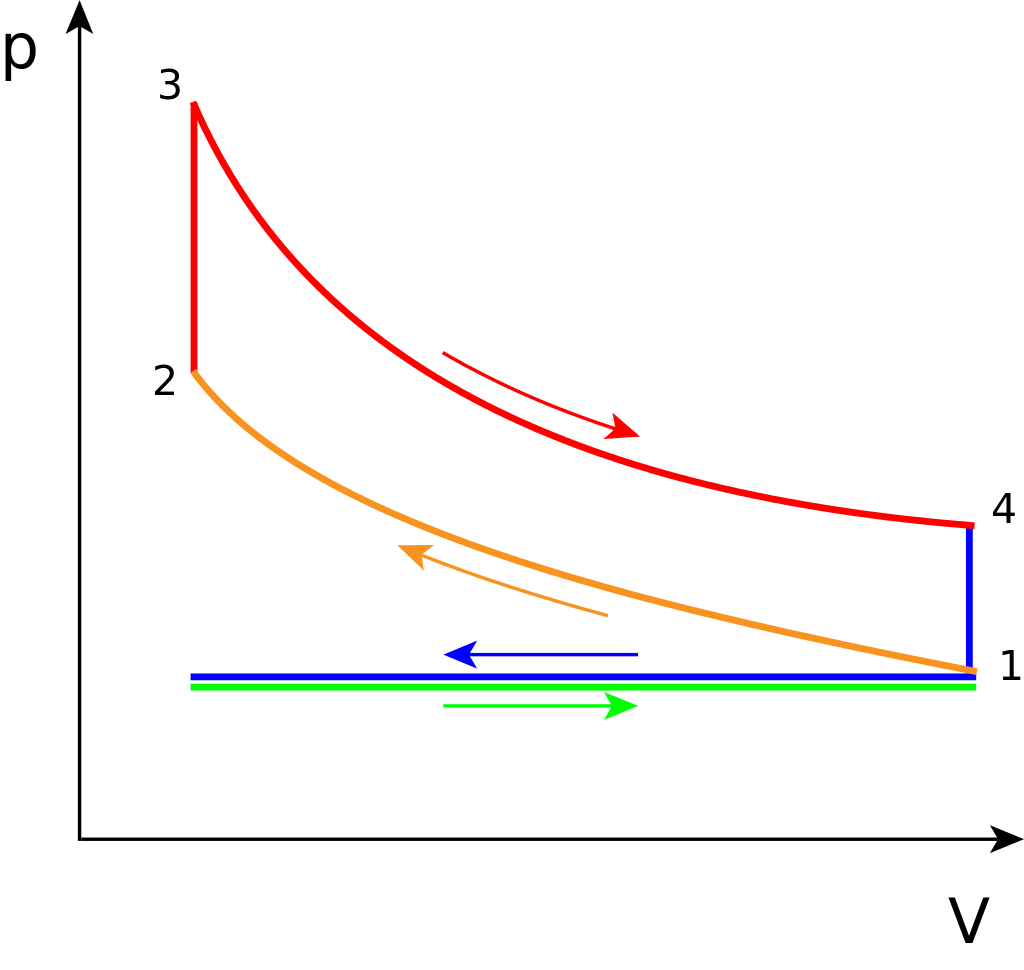
- 1$\rightarrow$ 2: ideal compression
- Adiabatic, PV work required by the engine.
- 2$\rightarrow$ 3: sensible energy added through burning of the fuel/air mixture
- Combustion assumed to occur quickly, at constant volume. Pressure rises.
- 3$\rightarrow$ 4: ideal expansion
- Adiabatic, PV work produced by the engine.
- 4$\rightarrow$ 1: heat rejection
- drop in pressure as the valve is opened at the bottom of the stroke.
- exhaust and intake are the horizontal blue and green lines.
Net work¶
- The net work produced is the area under curve 3$\rightarrow$4 minus the area under curve 1$\rightarrow$2.
- Since the compression and expansion are adiabatic, the work is equal to differences in internal energy $u$.
- Work required for compression: $W_c=u_2-u_1$.
- Work done by expansion: $W_e = u_3-u_4$.
- Net work performed by the engine = $W_e-W_c = (u_3-u_4)-(u_2-u_1)$.
Note that $u_2=u_3$ since process 2$\rightarrow$3 is adiabatic and constant volume. The "heat added" step is really sensible energy generated by combustion. But the internal energy of the mixture remains fixed.
Adiabatic compression and expansion.¶
- Assume ideal gas and adiabatic compression/expansion.
$$du = dW = -PdV$$
$du = c_vdT$ $$c_vdT = -PdV$$
$P = RT/V$, rearrange
$$\frac{dT}{T} = -\frac{R}{c_v}\frac{dV}{V}$$
- $R = c_p-c_v$, $\gamma = c_p/c_v$.
- $\rightarrow$ $R/c_v = \gamma -1$.
$$\frac{dT}{T} = -(\gamma-1)\frac{dV}{V}$$
- Assume $\gamma$ is constant. Then integrate to
$$\ln\frac{T_2}{T_1} = -(\gamma-1)\ln\frac{V_2}{V_1}$$
Rewrite as $$\frac{T_2}{T_1} = \left(\frac{V_1}{V_2}\right)^{\gamma-1}$$
Using $P=RT/V$, and expressions for $\gamma$ above, we have $$\frac{T_2}{T_1} = \left(\frac{P_2}{P_1}\right)^{(\gamma-1)/\gamma}$$
Similarly $$P_1V_1^\gamma = P_2V_2^\gamma$$
If we relax the assumption that $\gamma$ is constant, we have $$\ln\frac{V_2}{V_1} = -\int_{T_1}^{T_2}\frac{c_v(T)}{RT}dT$$
Example¶
- Compute the work and efficiency on a lower heating value basis for an Otto cycle with a stoichiometric methane-air mixture.
- Use a compression ratio (CR) of 10. That is $V_1/V_2 = V_4/V_3 = 10$
- code below requires streams.py and cantera
from streams import streams
strm = streams({"O2":1,"N2":3.76}, {"CH4":1}, 300, 300, 101325, "gri30.xml")
CR = 10
#----------- state 1: cold, atmospheric reactants
strm.set_gas_mixing_state(strm.ξst)
P1 = strm.gas.P
T1 = strm.gas.T
u1 = strm.gas.int_energy_mass
#----------- state 2: compress reactants
strm.set_gas_state_adiabatic_compression_expansion(1/CR)
P2 = strm.gas.P
T2 = strm.gas.T
u2 = strm.gas.int_energy_mass
#----------- state 3: burnt products
strm.gas.equilibrate("UV")
P3 = strm.gas.P
T3 = strm.gas.T
u3 = strm.gas.int_energy_mass
print(f'NO = {strm.gas.Y[strm.gas.species_index("NO")]*1000000:0f}')
#----------- state 4: expanded products
strm.set_gas_state_adiabatic_compression_expansion(CR)
P4 = strm.gas.P
T4 = strm.gas.T
u4 = strm.gas.int_energy_mass
print(T4, P4)
strm.gas.equilibrate("UV")
print(strm.gas.T, strm.gas.P)
print(f'NO = {strm.gas.Y[strm.gas.species_index("NO")]*1000000:.1f}')
#----------- work and efficiency
W = (u3-u4) - (u2-u1) # J/kg mixture
LHV = strm.get_LHV_pCC() # J/kg fuel
η = W/strm.ξst/LHV # efficiency; ξst is used to convert W from J/kg mix to J/kg fuel
print(f"η = {η:.2f}")
print(f'P1 = {P1/101325:.2f} atm, T1 = {T1:.0f} K')
print(f'P2 = {P2/101325:.2f} atm, T2 = {T2:.0f} K')
print(f'P3 = {P3/101325:.2f} atm, T3 = {T3:.0f} K')
print(f'P4 = {P4/101325:.2f} atm, T4 = {T4:.0f} K')
NO = 7249.681704 1581.0497304280195 541668.9741244201 1834.455938236005 619897.2037123383 NO = 193.1 η = 0.43 P1 = 1.00 atm, T1 = 300 K P2 = 23.02 atm, T2 = 691 K P3 = 96.24 atm, T3 = 2846 K P4 = 5.35 atm, T4 = 1581 K
- A compression ratio of 5 gives $\eta=0.33$
- $P_2=9$ atm, $T_2=546$ K
- A compression ratio of 10 gives $\eta=0.43$
- $P_2=23$ atm, $T_2=690$ K
- At high CR, the high $T_2$ can lead to auto-ignition and engine knock, which can cause damage.
- For methane-air, $\gamma=1.37$
Octane rating¶
- See Wikipedia for lots of information
- The octane number is the percent of iso-octane (by volume) in a mixture of iso-octane and n-heptane, that has the same knock characteristics as the given fuel.
- A higher octane number indicates a fuel that is more resistant to knock.
- There are several different measurement methods, including the "Research Octane Number" and the "Motor Octane Number", an average of which is used in the U.S.
- It is possible to have an octane number greater than 100.
- Higher octane numbers can tolerate higher compression ratios.
- Elevation matters.
Review article on impact of fuel molecular structure on auto-ignition¶
Diesel cycle¶
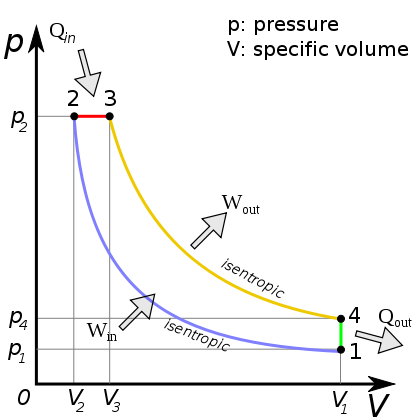https://en.wikipedia.org/wiki/Diesel_cycle#/media/File:DieselCycle_PV.svg
- 4 strokes
- Compress only air $\rightarrow$ hot
- Then inject fuel $\rightarrow$ autoignition, but the injection timing is controlled.
- No knock issue, allows cheaper fuels.
- High compression radio gives higher efficiency.
- CR = 12-24.
- In the diagram above, the combustion step 2$\rightarrow$ 3 occurs with some piston travel $\approx$ constant pressure.
- Heat steps $Q$ again refer to release of sensible energy, and exhaust/intake.
- In the code above, change the
equilibrate("UV")toequilibrate("HP")
Other cycles¶
- Brayton cycle (gas turbines)
- Rankine cycle (steam cycle, e.g., coal plants)
Fuels¶
Compare diesel fuel and gasoline
Diesel: about 25% aromatics, $C_{12}H_{23}$, ($C_{10}H_{20}$ - $C_{15}H_{28}$)
Gasoline: about 35% aromatics, $C_8H_{18}$, ($C_4$ - $C_{12}$)
$\rho_D\approx 0.85$ kg/L, versus $\rho_G\approx 0.72$ kg/L
Heating value: $HV_D\approx 38.6$ MJ/L versus $HV_G\approx 34.9$ MJ/L
Heating value: $HV_D\approx 45.4$ MJ/kg versus $HV_G\approx 48.5$ MJ/kg
On an equal mass basis, the large differences in efficiency are due to diesel having higher compression ratios.
Ethanol additives reduces hydrocarbon emissions (volatile organic compounds, VOCs)
Exhaust gas recirculation (EGR)¶
- $NO_x$ is a pollutant formed at high temperatures.
- To reduce $NO_x$, reduce peak flame temperatures.
- One way to do this is by recirculating cool exhaust gases into the reaction mixture. This increases the heat capacity and reduces the flame temperature.
- Also reduces efficiency.
- Very common in diesel engines.
- Up to 50% EGR
- In SI engines, only 5-15% EGR
Recuperation/Regeneration¶
- Raise flame temperatures by preheating reactants (air).
- Exchange heat with hot combustion products.
- High temperature applications, glass furnaces.
https://www.glassonweb.com/news/nsg-cold-repair-float-glass-furnace-us
1-(T1/T2)*(T4/T1-1)/(T3/T2-1)
0.405768344464696