Problem 1
Assuming natural gas is pure methane, compute the pounds of CO$_2$ emitted per MMBTU heating value assuming stoichiometric combustion to products of complete combustion.
Problem 3
For the Skyline coal composition provided in the notes, compute the pounds of CO$_2$ emitted per MMBTU heating value assuming stoichiometric combustion to products of complete combustion. Compare your results of this problem to those of Problem 2.
Problem 4
For the Skyline coal composition provided in the notes, assuming combustion with excess air resulting in 3% O$_2$ (by mole) in the exhaust on a dry basis, if all the N in the coal is converted to NO, what is the NO concentration in ppmv?
Problem 5
Find an article on coal or natural gas. Read the article and include a link to it. Write a one page summary discussing key points in the article. Do you agree with the points made?
Problem 6
A 50 $\mu$m coal particle is injected into a furnace. The initial particle temperature is 170 $^o$F (350 K). Estimate the initial heating rate (K/s) of the particle due to radiative heat transfer, and due to conductive heat transfer. Do this as a function of the environment temperature and plot the heating rate versus environment temperature ranging from 500 to 3000 K. Include curves for radiative and convective heating on the same plot. Assume the particle is at the same velocity as the surrounding as so that the Nusselt number is 2. Assume the coal density is 1300 kg/m$^3$. Assume a particle emissivity of 0.5. Assume the particle heat capacity is 1400 J/kgK. For the furnace gas, you can use a thermal conductivity of 0.03 W/mK (air), though using a value at the mean temperature between the gas and the particle is better (this can be done easily with Cantera).
The Nusselt number is defined as $Nu = hd/k$, where $h$ is the heat transfer coefficient, $d$ is the particle diamter, and $k$ is the gas thermal conductivity.
The particle energy equation for radiation is $$mc_p\frac{dT}{dt} = \epsilon A\sigma(T_g^4 - T_p^4).$$
The particle energy equation for convection is $$mc_p\frac{dT}{dt} = hA(T_g - T_p).$$
A timescale can be defined as $$\tau = \frac{\left|\Delta T\right|_{max}}{\left|\frac{dT}{dt}\right| _{max} }$$
Here,
$$\left|dT/dt\right|_{max}$$
will be the initial heating rate you computed above, and
$$\left |\Delta T\right |_{\text{max}}$$
is simply the surrounding temperature - initial particle temperature. In addition to your heating rate plot, made another plot with the timescale (in ms) for radiative and conductive heating versus temperature. Plot the y-axis (timescale) on a log scale.
Problem 7
Label the following list with the corresponding number in the figure
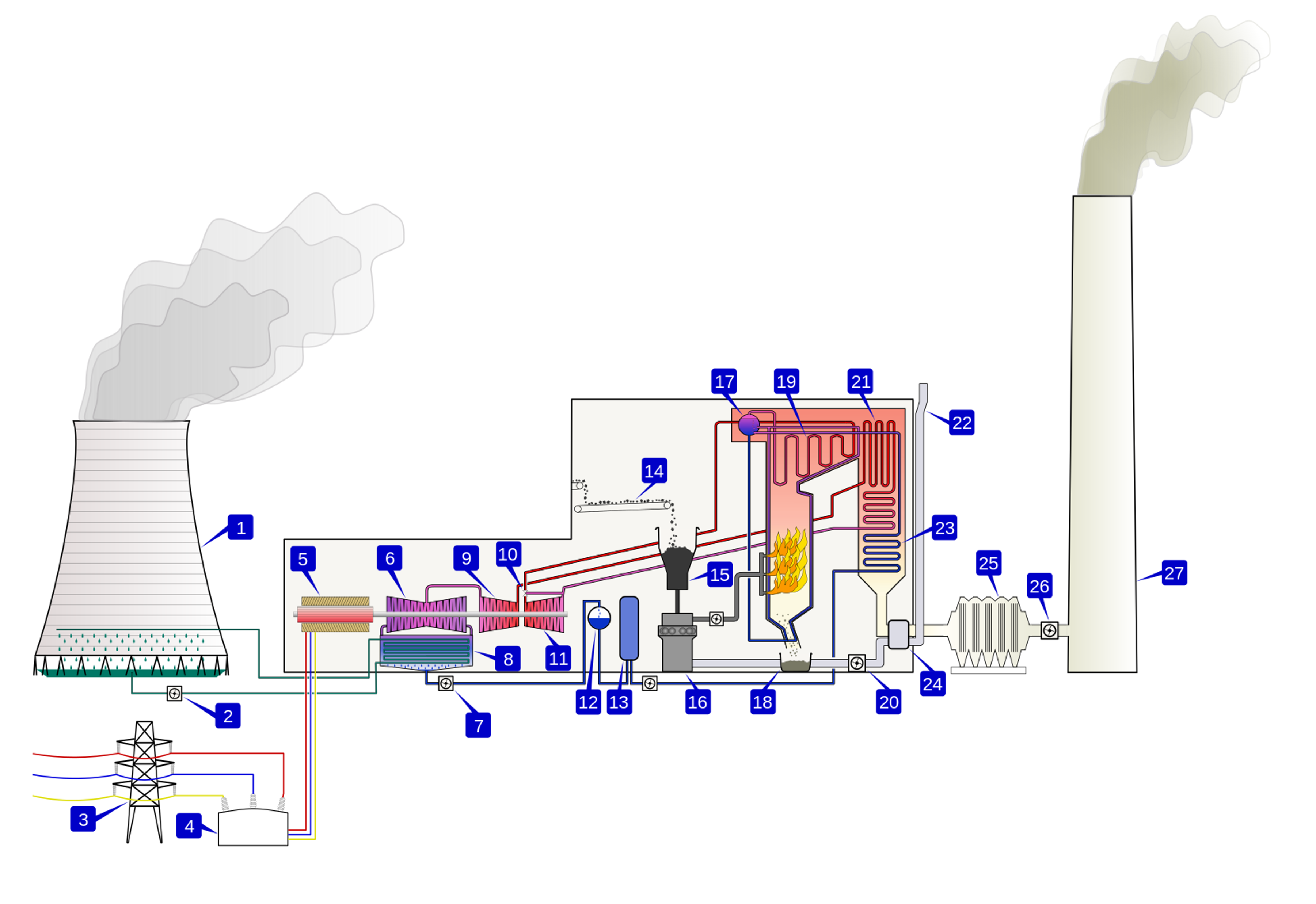
| Unit | number |
|---|---|
| forced draught fan | |
| boiler feed pump | |
| coal hopper | |
| cooling tower | |
| pulverised fuel mill | |
| air intake | |
| cooling water pump | |
| particle precipitator | |
| low pressure turbine | |
| induced draught fan | |
| coal conveyor | |
| chimney stack | |
| condenser | |
| superheater | |
| economiser | |
| generator | |
| pylon (termination tower) | |
| feed heater | |
| high pressure turbine | |
| air preheater | |
| deaerator | |
| ash hopper | |
| reheater | |
| steam governor | |
| intermediate pressure turbine | |
| unit transformer | |
| boiler drum |