Problem 1, this
Post a picture of your favorite electric power plant. Any type: nuclear, solar, wind, coal, natural gas, hydroelectric, etc. If you don’t have a favorite, then get one! Also, tell us something interesting about it, and tell us why you like it. (Listing the power output is not very interesting.)
Problem 2
What is the terminal settling velocity of a 2.5 $\mu$ particle?
Problem 3
Draw PV and TS diagrams for the Carnot refrigeration cycle. Outline the steps. What is the thermodynamic efficiency for an average Provo high temperature in July?
Problem 4
An entropy balance is given by $$\Delta S = S_{in} - S_{out} + S_{gen}.$$ Is $S_{gen}$ greater than, less than, or equal to zero for a real process? Here, $S$ is the rate of entropy. Consider the following image:
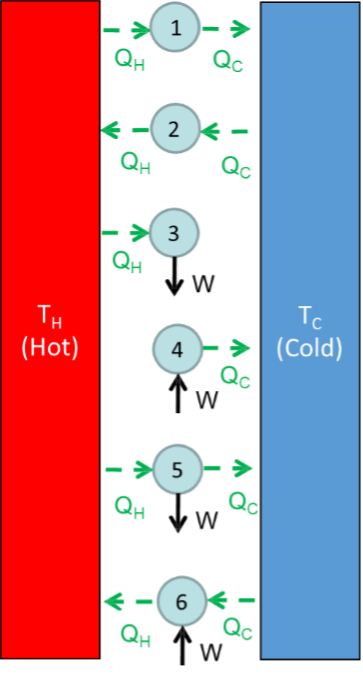
Determine if each system is feasible. If it is, find an example for the system (e.g., heat engine, electric heater, etc.).
Problem 5
What is the difference between a refrigerator and a heat pump?
Compare the power requirements of an electric heater and a Carnot heat pump used to heat a house to 20 $^oC$ with an outside temperature of 0 $^oC$.
Problem 6
Compute thermal efficiencies of the ideal Carnot, Otto, Diesel, and Brayton cycles for high and low temperatures of 1800 K and 300 K. Use a a compression ratio of 12 for Otto and Diesel, and a pressure ratio of 12 for Brayton.
Problem 7
Compare the Otto engine efficiency computed using the simple air standard assumptions with a more complex equilibrium calculation using the assuming a stoichiometric methane-air mixture with 300 K and 1 atm ambient conditions. Use a compression ratio of 12. Here’s a link to a jupyter notebook that gives some basic Cantera use. You will need to have Cantera installed, or use Google Colab .