ChEn 433
Class 25 Hydro, Geothermal
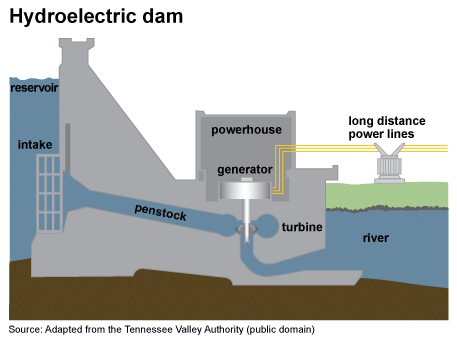
Hydropower
- Hydroelectric
- 1870 Cragside Dam in Rothbury, England
- Dams: regulating flows, flood control, storage
- Historically used for mechanical energy
- Renewable
- No fuel costs
- Wave
- Tidal
Hydropower
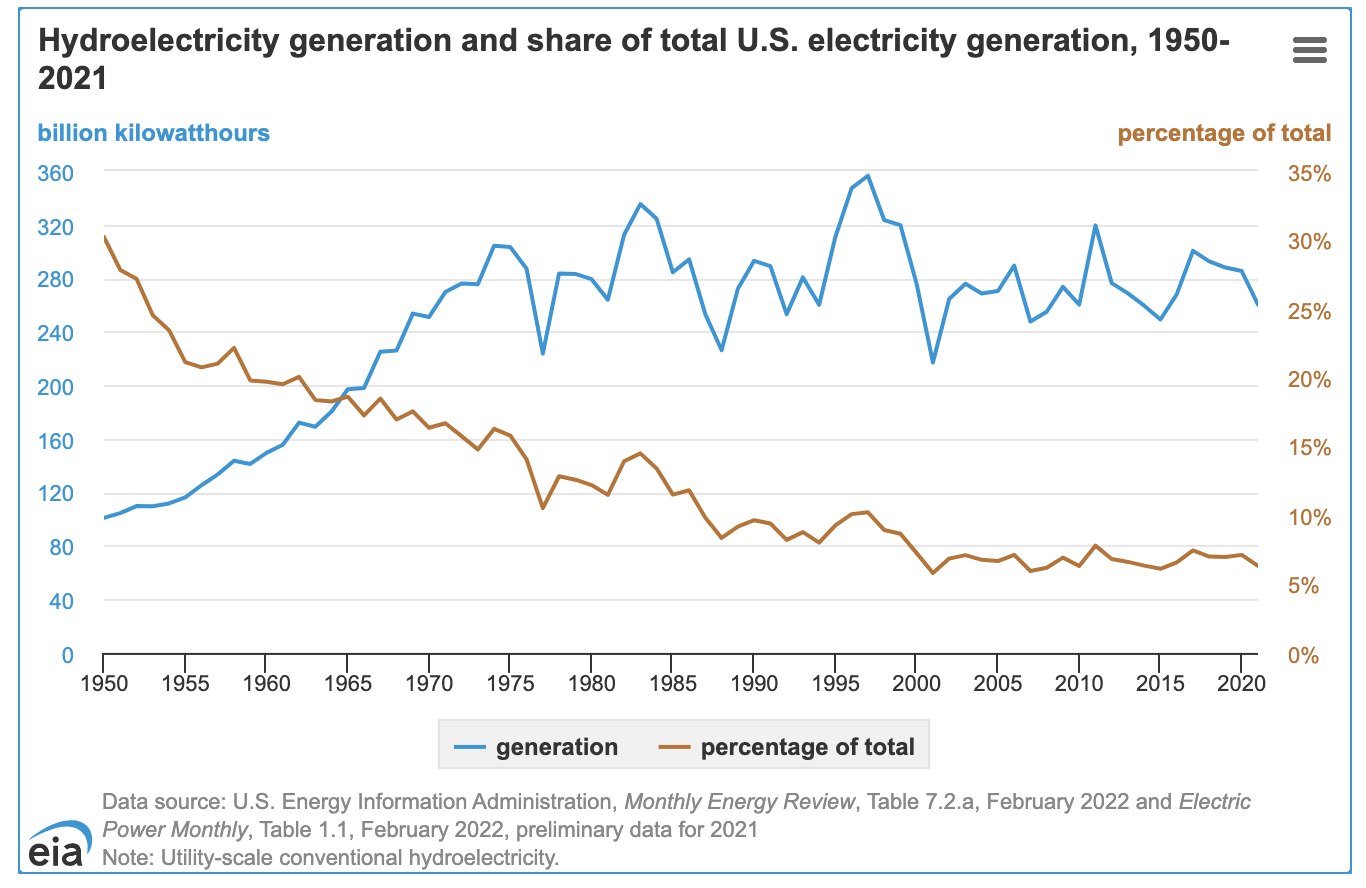
- 6.3% of US
electricity
- 30% in 1950
- 31.5% of US renewable electricity
Hydropower
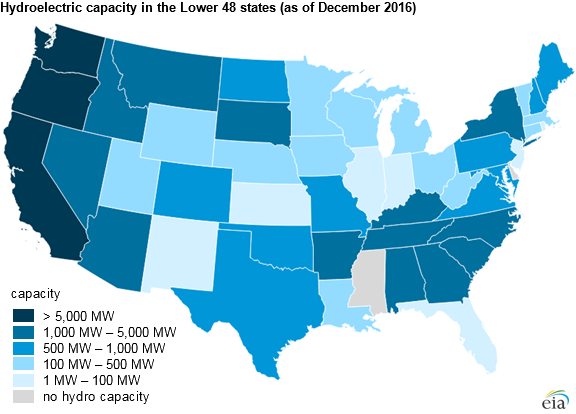
US Hydropower
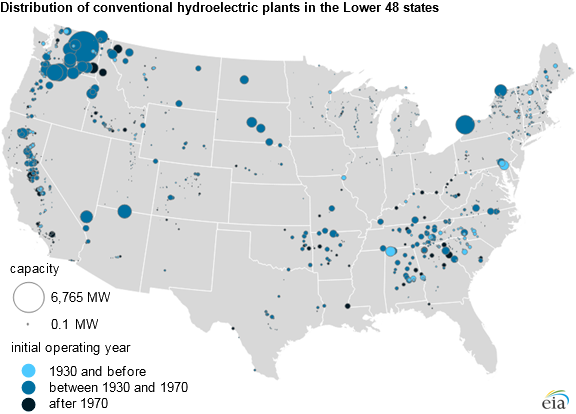
US Hydropower
Three Gorges Dam
- China
- $32 billion
- 181 m
- 22.5 GW (11x Hoover)
- Nine year construction to 2012
- 34 Francis turbines
- > 1.3 million people
displaced
- 1500 cities/towns/villiages along the river
- Issues:
- erosion, sedimentation, landslides,
- waste,
- wildlife


Simple Theory
\[\dot{W} = \dot{m}gh\] Power is the rate of potential energy change as the liquid falls under gravity over height \(h\).
Mechanical Energy Balance \[\dot{m}\left(\frac{P_1}{\rho} + \frac{v_1^2}{2} + gz_1\right) - \dot{W}_\text{turbine} = \dot{m}\left(\frac{P_2}{\rho} + \frac{v_2^2}{2} + gz_2\right)\]
Exercise
The average American home uses 893 kWh per month, which is 1.22 kW.
How many gallons per minute is needed to power the average home for a reservoir height of 100 m?
import pint; u = pint.UnitRegistry()
W = 893 * u.kW*u.hr/u.month
h = 100 * u.m
rho = 1000 * u.kg/u.m**3
g = 9.81 * u.m/u.s**2
print(f"W = {W.to(u.kW):.2f}")
# W = mdot * g * h
mdot = W / g / h
Vdot = mdot / rho
print(f"Vdot = {Vdot.to(u.gal/u.min):.2f}")19.75 gal/min
Capacity factors
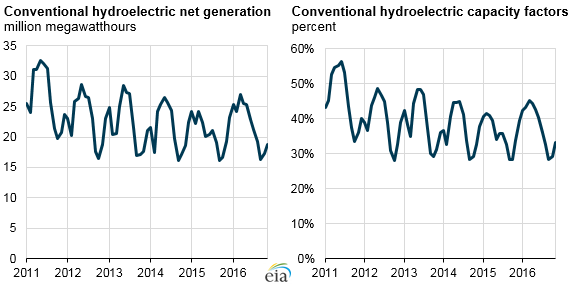
The amount of power generated each year from the nation’s hydroelectric facilities varies by the water available in dams and rivers. Many reservoirs must balance power output with competing water demand for irrigation, municipal, industrial, and other needs, as well as concerns with fish migration. As a result, hydroelectric facilities often do not run at full output. U.S. hydroelectric capacity factors, which measure actual output as a percent of total capacity, average between 30% and 40%. –EIA.gov
Article: Drought
Turbine types

Turbine types
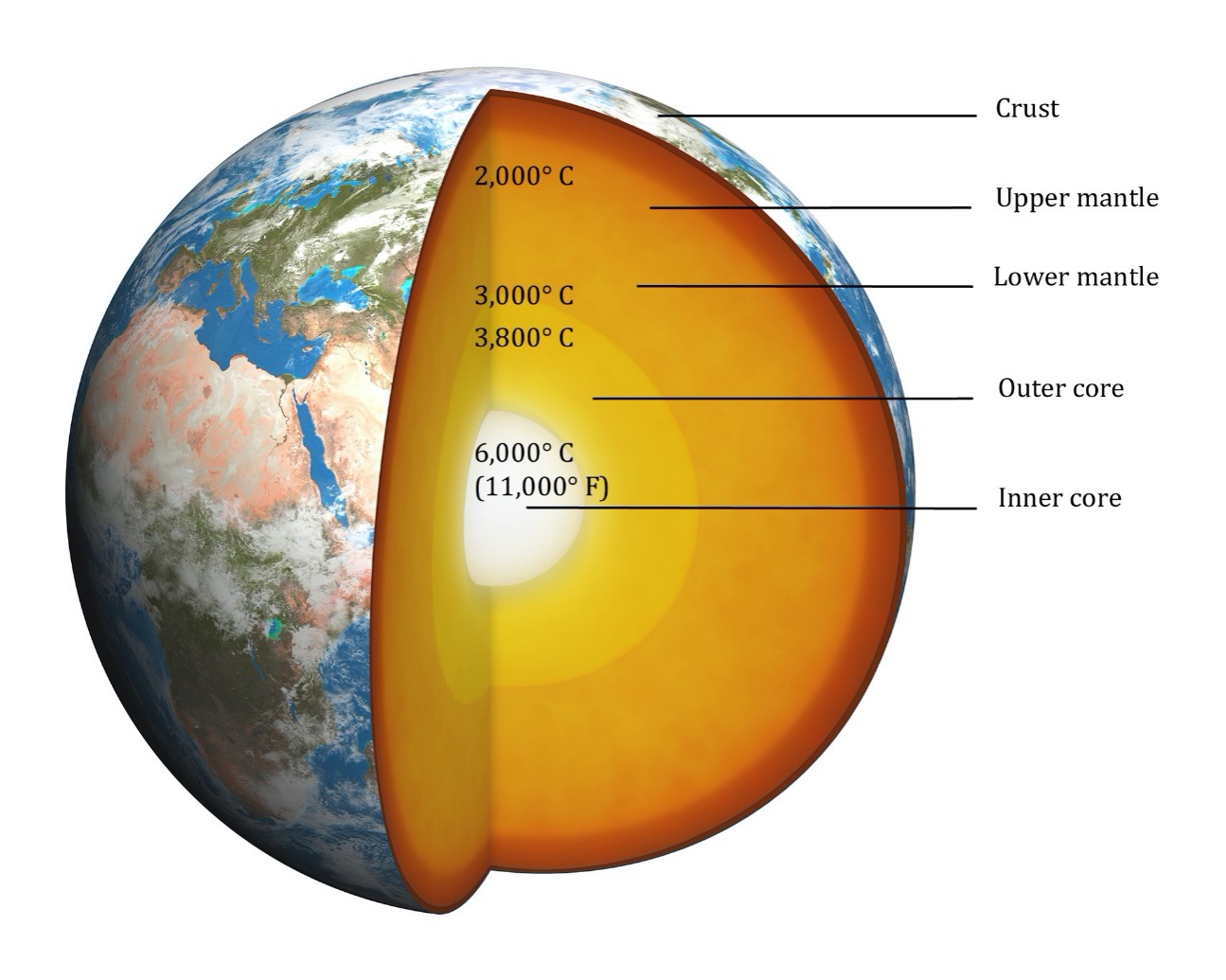
Earth core
- 99% of the earth is > 1000 \(^o\)C
- Heated by radioactive decay
- P up to 4 Mbar
- 0.07, 0.1 W/m\(^2\) (land, ocean)
- 9.2 CMO/yr
- total heat energy 1.26E31 J
- 5.4E27 J in the crust
- Thermal gradient ~25 \(^o\)C/km (100 \(^o\)C at 4 km).
Geothermal plants
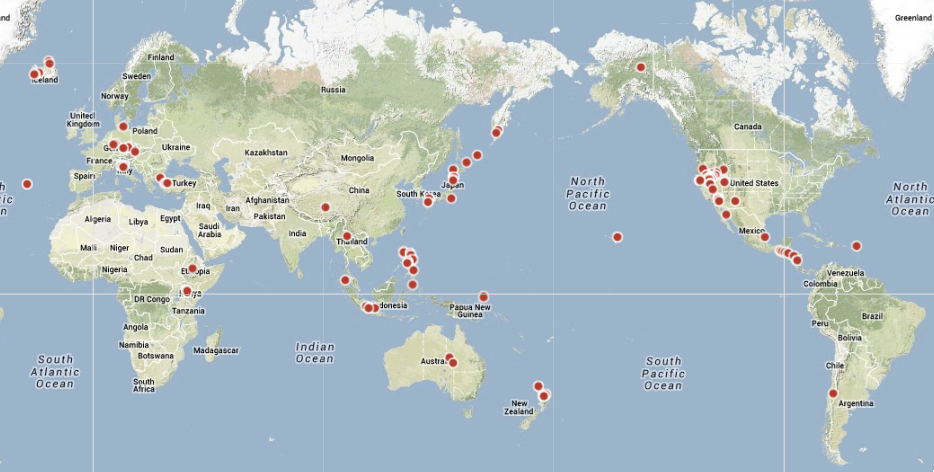

- The the prevalence of plants around the “ring of fire”
US Geothermal potential
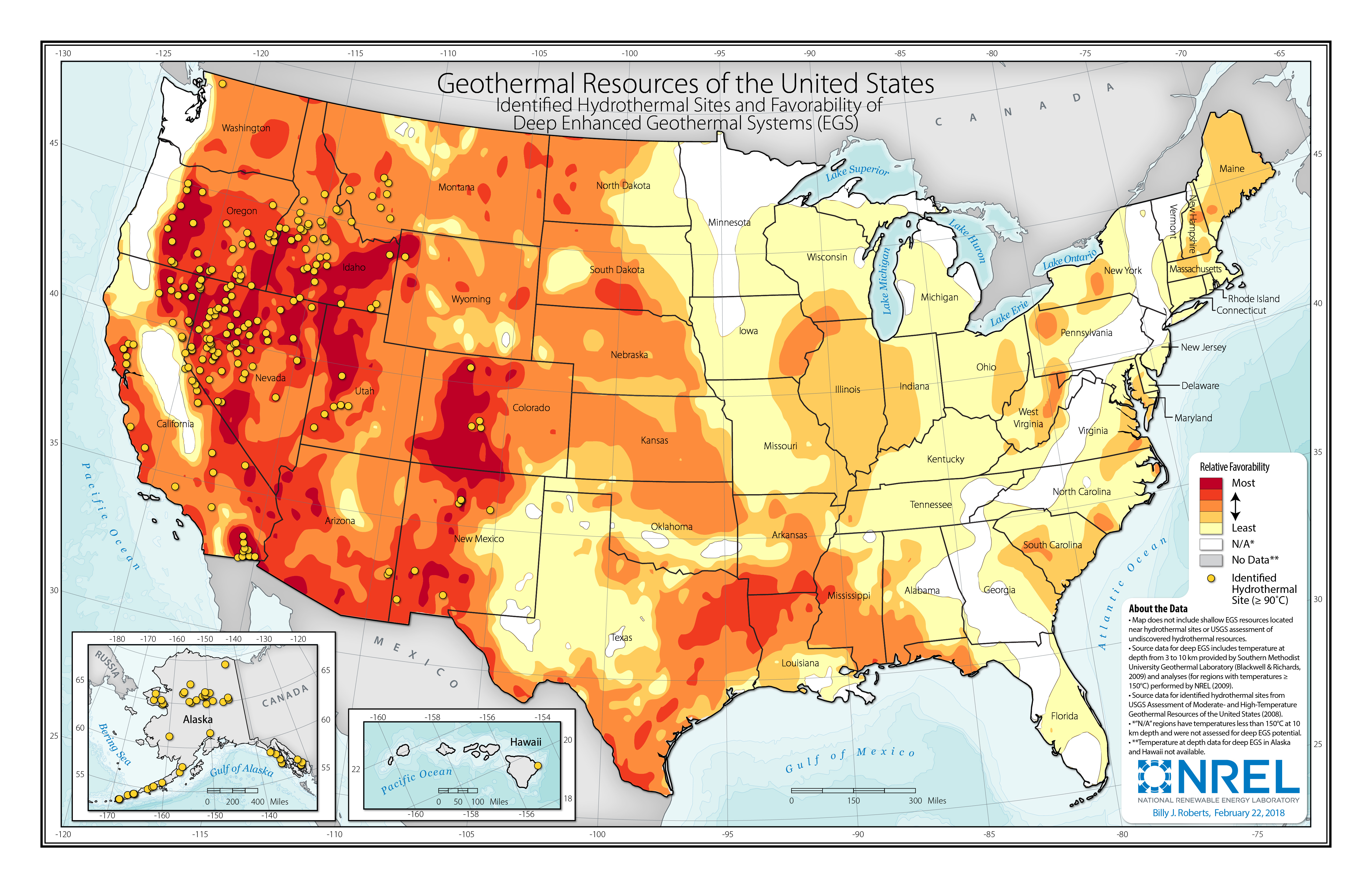
Geothermal production (direct heat)
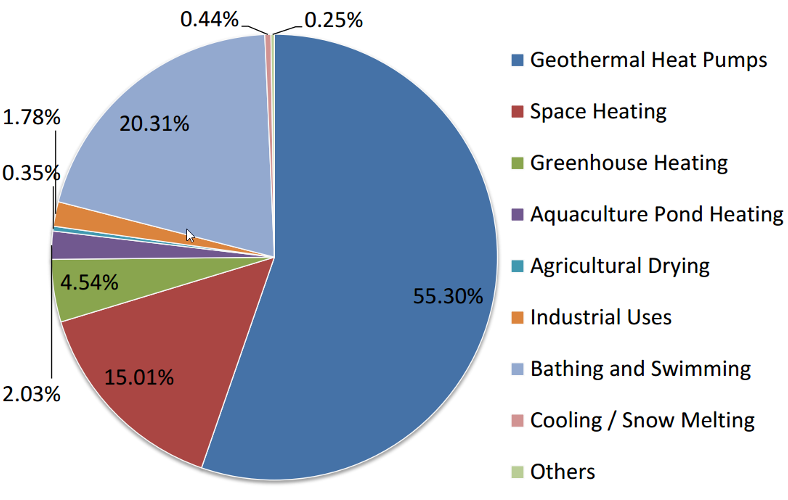
Lund and Boyd, Direct Utilization of Geothermal Energy 2015 Worldwide Review, World Geothermal Congress, 2015
Geothermal heat, power
- Two applications
- Direct heat
- Electricity generation
- First geothermal plant: Tuscany Italy 1904
- Average size > 10 MW = 153 MW
- Types: dry, flash (most common), binary
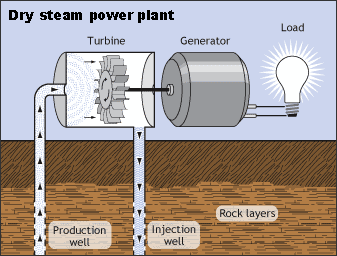
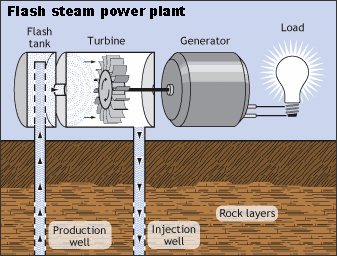
Geysers Geothermal Complex
- Northern California
- Largest plant
- 18 units
- 1.6 GW
- Dry steam
- 78 km\(^2\) land area
- 53% capacity factor

Hot dry rock (HDR)
- Summary of papers and articles
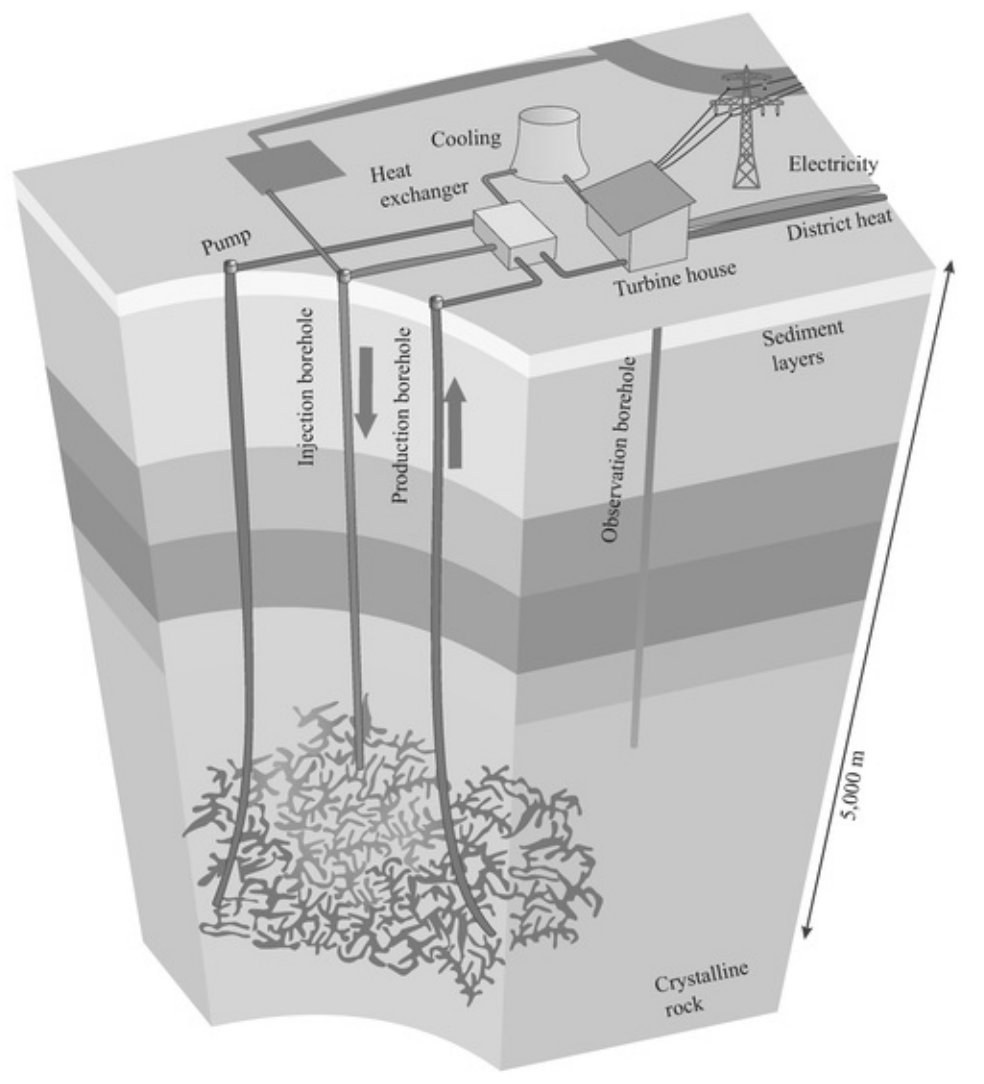
- Enhanced geothermal system (EGS)
- No natural water table
- Rock fracturing
- Two wells drilled: injection and production
- Depth issues
Issues
- Renewable
- Environmentally benign (other than land use)
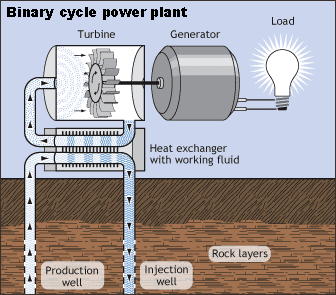
- Lower temperatures use the organic Rankine cycle (ORC)
- Low efficiencies at lower temperatures \(\rightarrow\) direct heat is more cost effective
- Drilling costs
- Resource depletion (run out of steam \(\rightarrow\) inject water, e.g., Geysers Complex)