ChEn 433 Solar
Class 21-22
Solar energy
What are the major themes and issues with solar power?
- Intermittent
- Cloud cover
- Energy storage
- Materials availability
- Land use requirements
Solar Energy
- Two major types
- solar thermal
- photovoltaic
- Wind and hydro power may be considered indirect solar energy.
- Outline
- Solar radiation physics
- Solar thermal
- Photovoltaics
- Implementation and contributions to world energy
- Economics
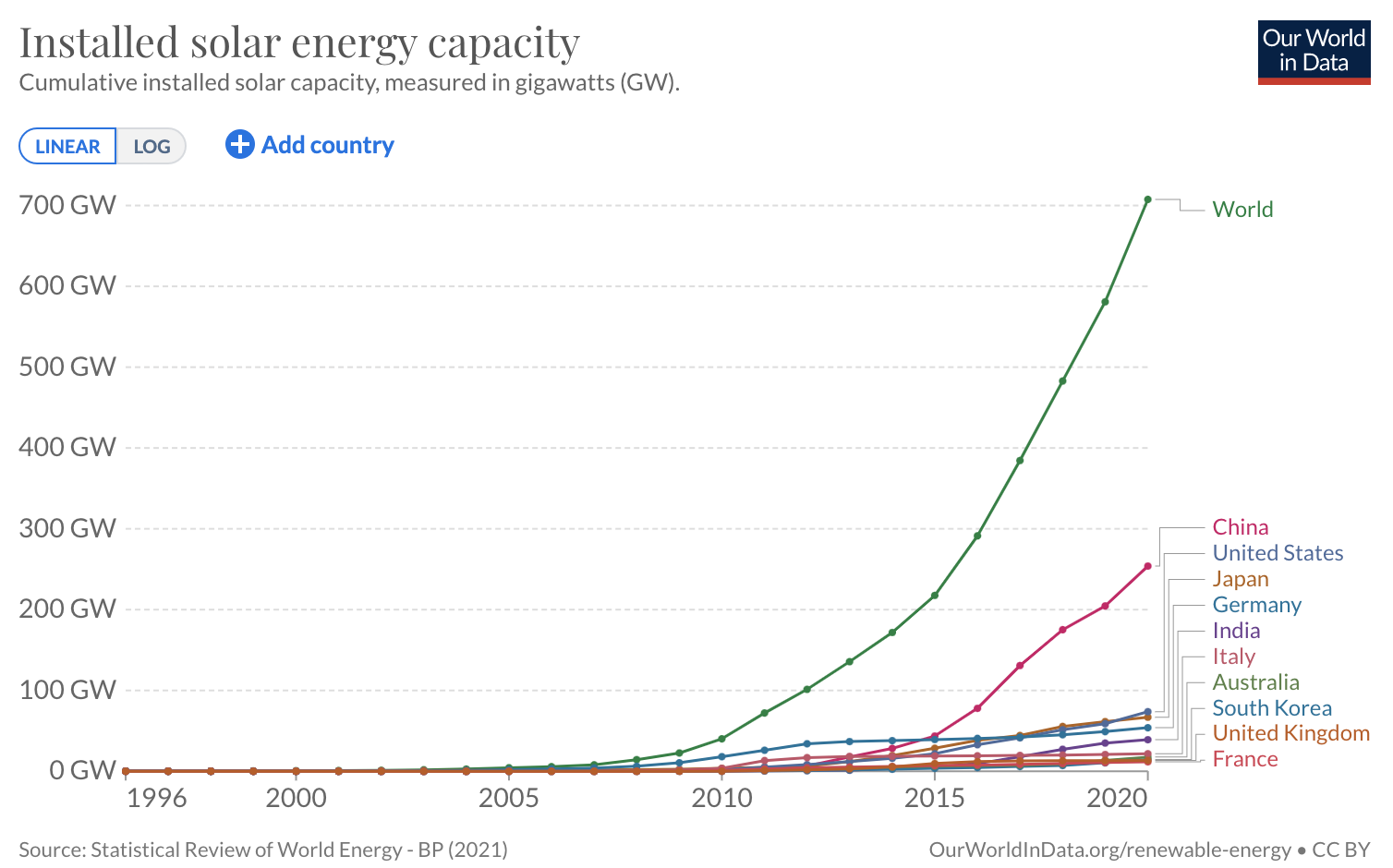
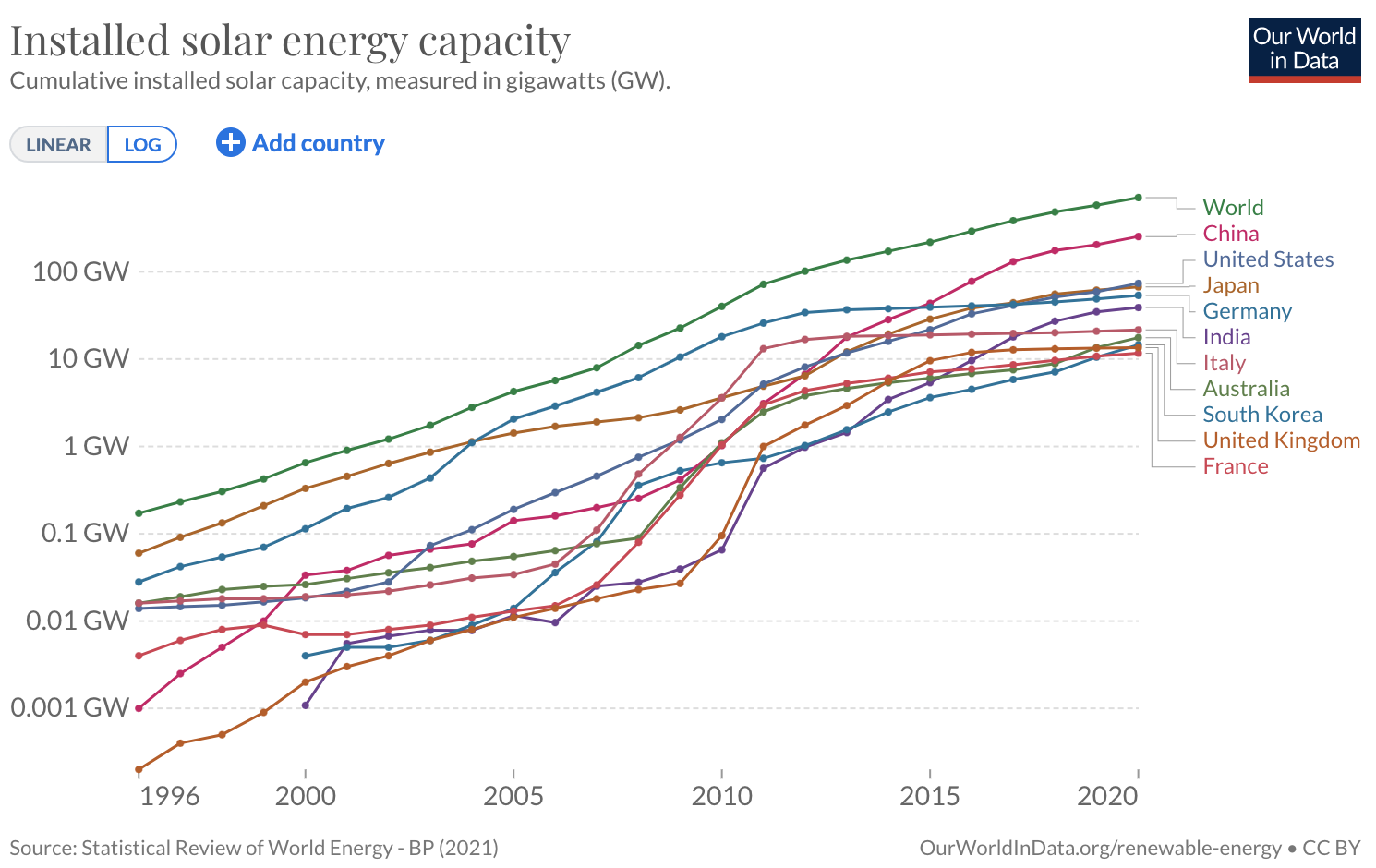
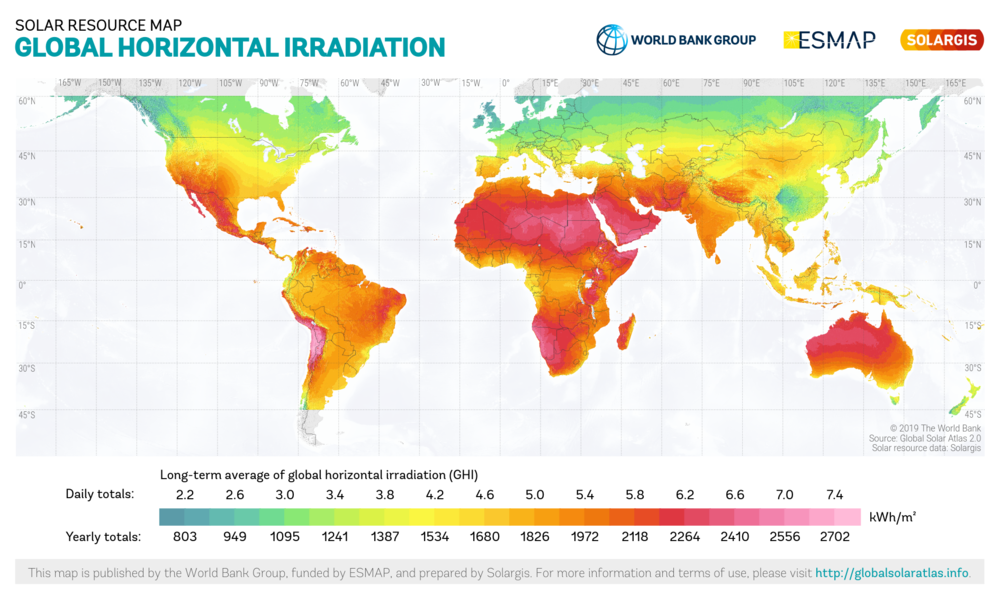
World solar energy
Solar is growing fast, and is 4.5% of world electricity
World solar energy
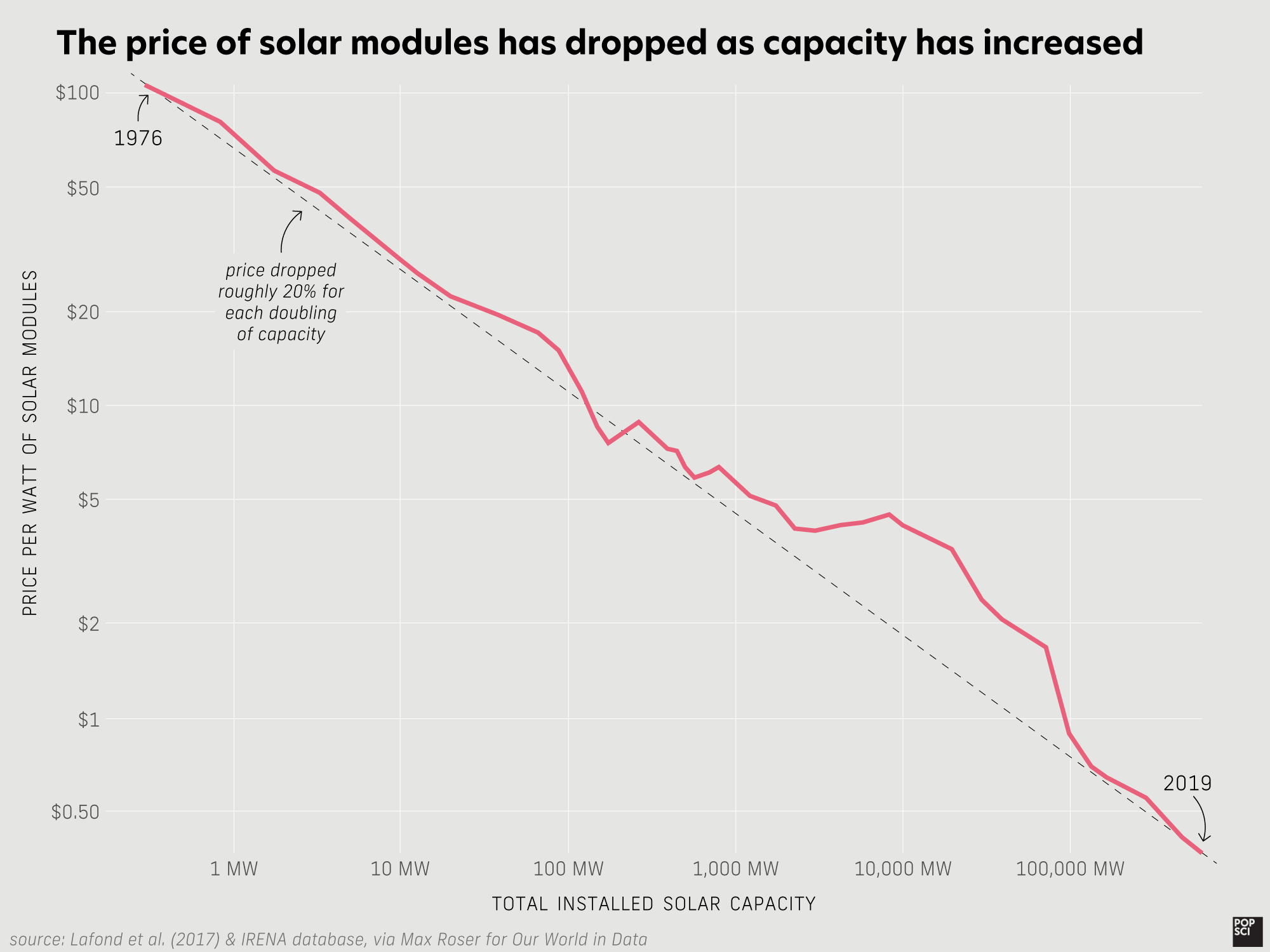
Economics

“The levelized cost of energy (LCOE) is a measure of a power source that allows comparison of different methods of electricity generation on a consistent basis. The LCOE can also be regarded as the minimum constant price at which electricity must be sold in order to break even over the lifetime of the project.”
LCOE
Economics
1 CMO
- 47 billion solar panals
- 450 W (72 cell panel)
- Area = 2.06 m\(^2\)
- using 24% capacity factor (avg in US)
- 268,000 per hour for 20 years
- American power use 1.23 kW (avg)
- Current
world electricity use = 0.626 CMO (29165 TWh)
- (Energy Institute Statistical Review of World Energy).

2 kW solar plant
3.5 CMO
If all the highways, streets, buildings, parking lots and other solid structures in the 48 contiguous United States were pieced together like a giant jigsaw puzzle, they would almost cover the state of Ohio (Reference)
Rate of growth (articles)
Human cost (article)
Greenhouse gases from metals (article)
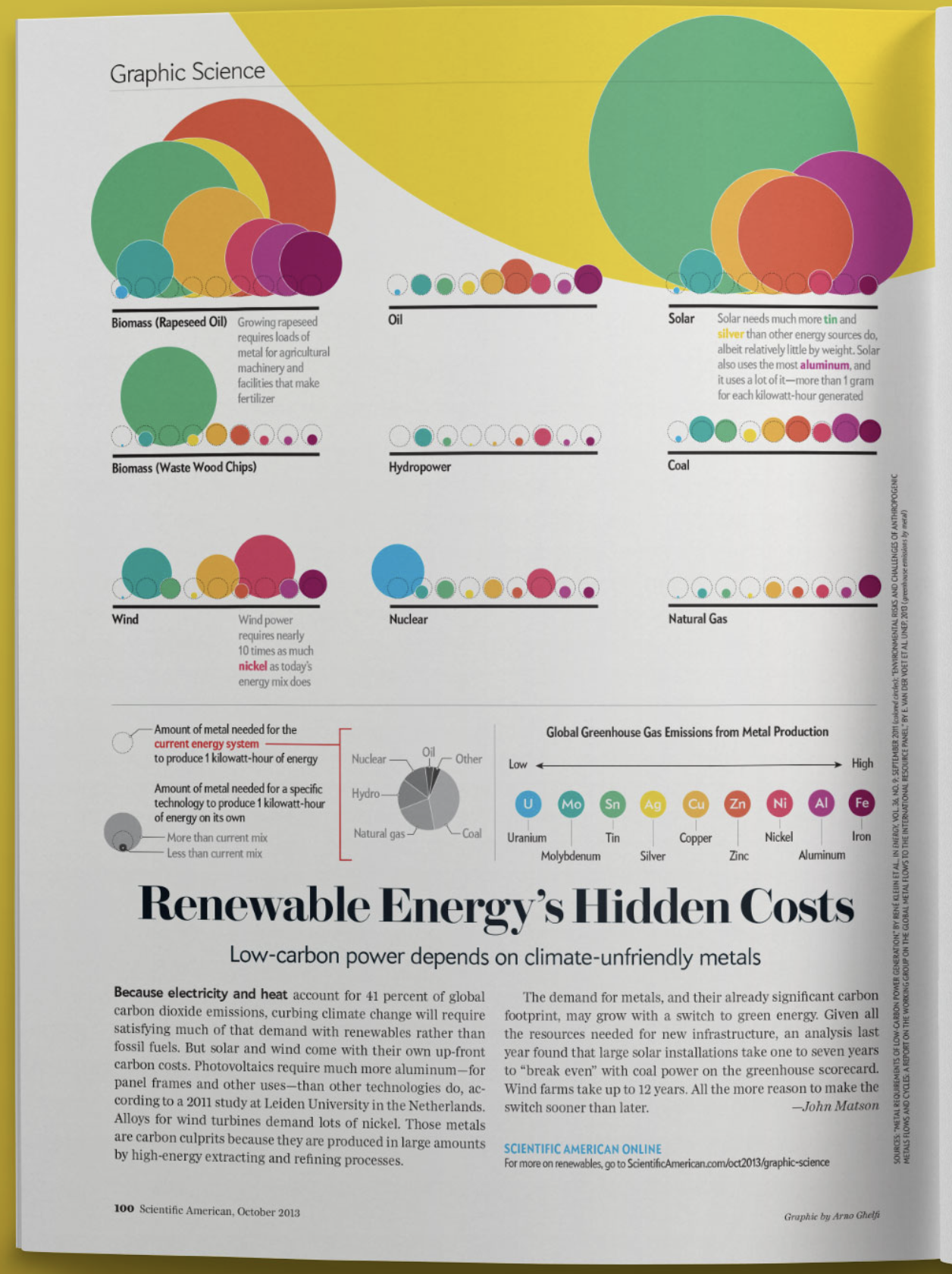
Large solar installations take one to seven years to “break even” with coal power on the greenhouse scorecard
Break even (article)
The Sun
Nuclear fusion \[4^1_1p \rightarrow
_2^4\alpha + 2e^+ + 2\nu_e +\Delta E\]
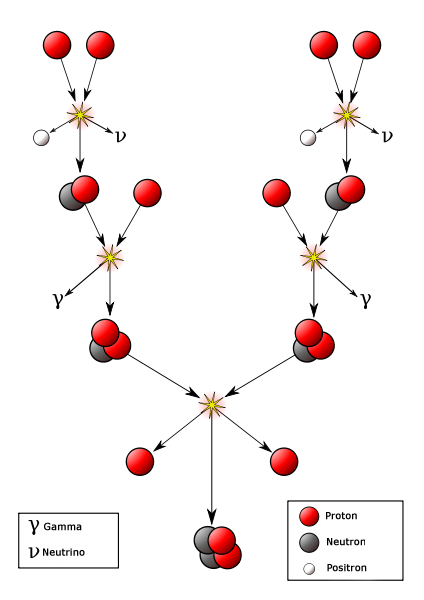
\[\Delta E = 3.955\times 10^{-12}\, J\, =
24.687 MeV\]

- Energy released = \(3.8\times
10^{26}\) W
- E per Area = \(63.3\) MW/m\(^2\)
E at Earth = \(1361\) W/m\(^2\) solar constant
Radiative Spectrum

Radiative Spectrum
- \(E = \sigma T^4\rightarrow T=5777\) K
- Distribution
- 7% ultraviolet (UV)
- 47% visible
- 46% infrared (IR)
- Atmospheric losses
- reflection
- absorption: O\(_3\), H\(_2\)O, O\(_2\), CO\(_2\)
- Rayleigh scattering: molecules \(d\ll\lambda\)
- Mie scattering: particles (pollution) \(d\gg\lambda\)

Air mass
- AM is (relative) mass of air light travels through \[AM = \frac{1}{\sin\gamma_s}\]
- time of day, year
- Summer, winter
- Zenith angle is \(90^o-\gamma_s\)
- =
latitude - solar declination angle
- at solar noon
- latitude is measured from the equator
- positive toward the north
- -23.45\(^o\) < declination angle < 23.45\(^o\)
- winter, summer
- =
latitude - solar declination angle
- \(\gamma_s\) is angle of sun from horizontal (elevation)
- \(\alpha_s\) is the solar azmuth
Air mass
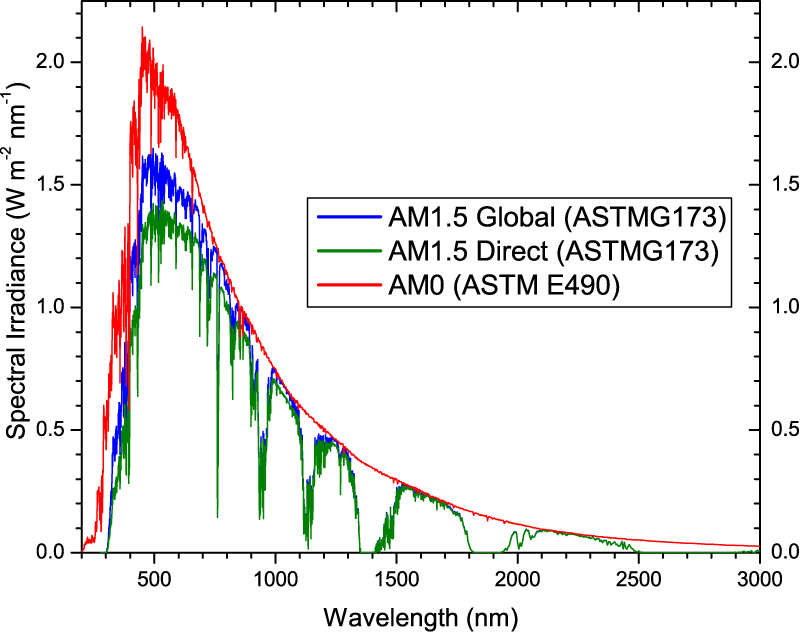
- Standard spectrum at AM1.5 \(\rightarrow\) 1000 W/m\(^2\)
Air mass
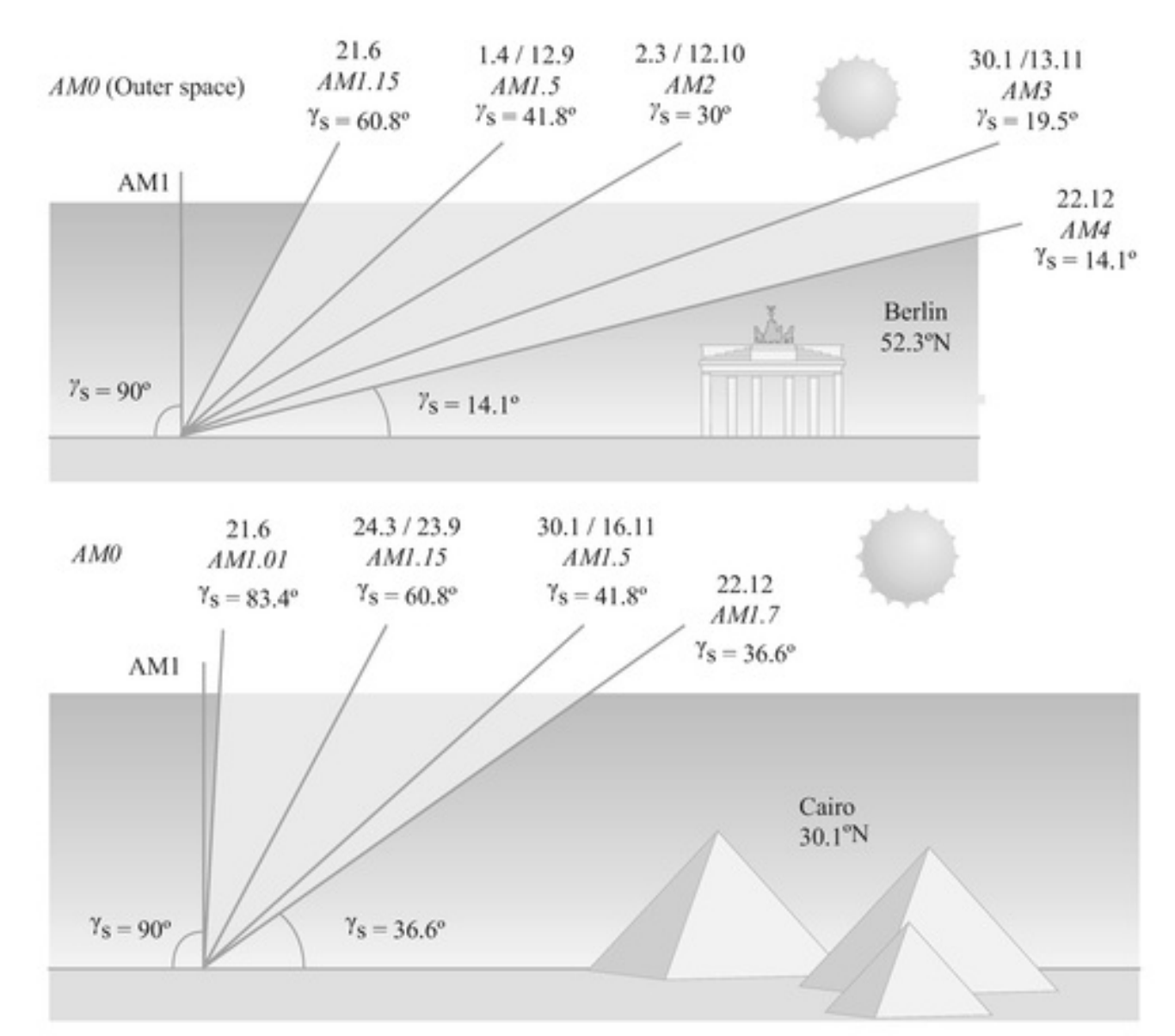
Effect of solar angle


- plot is for Athens
- June:Dec = 40:1 in Bergen, Norway
- June:Dec = 3.3:1 in Lisbon, Portugal
Tracking solar panels
![]()
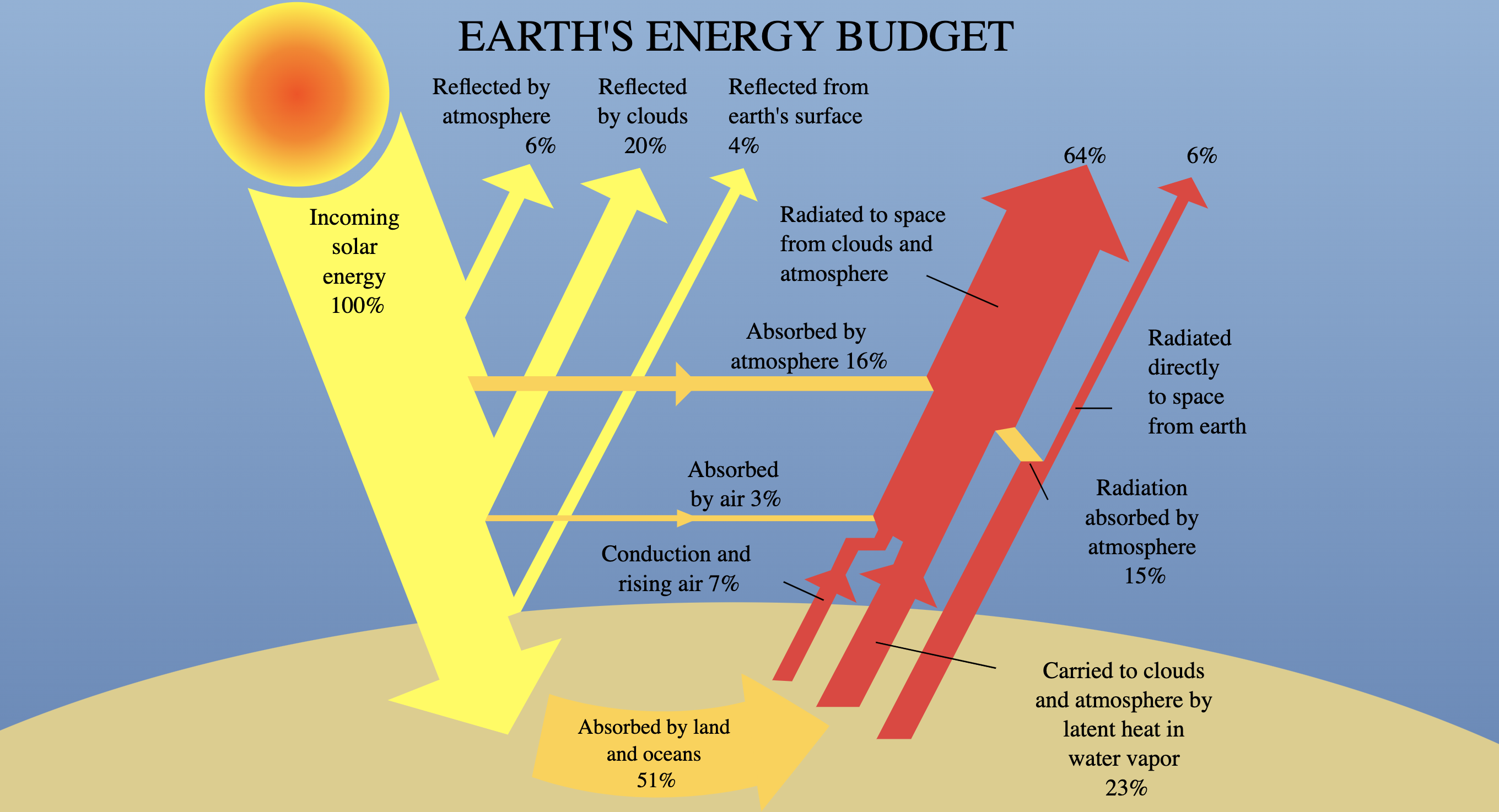
Earth energy balance
Albedo

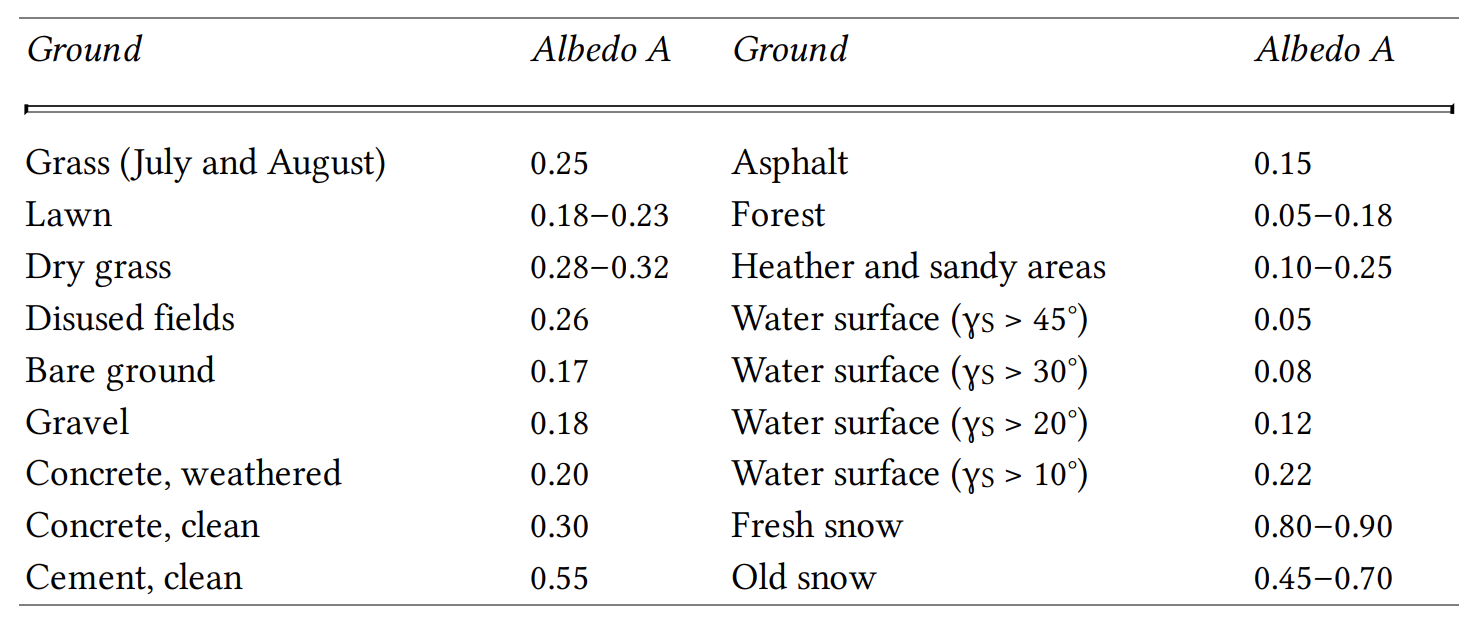
Rank order the albedo of the following surfaces:
| Surface |
|---|
| Forest |
| Fresh Snow |
| Water (\(\gamma_s > 45^o\)) |
| Bare ground |
| Clean cement |
Albedo is the proportion of incident light or radiation that is reflected by a surface, typically a planet or moon.
Albedo

Rank order the albedo of the following surfaces:
| Surface | Albedo |
|---|---|
| Water (\(\gamma_s > 45^o\)) | 0.05 |
| Forest | 0.1 |
| Bare ground | 0.2 |
| Clean cement | 0.55 |
| Fresh Snow | 0.85 |
Albedo is the proportion of incident light or radiation that is reflected by a surface, typically a planet or moon.
Albedo

Solar irradiance
- 11 year cycle (changes in the sun’s magnetic field)
Solar irradiance
- Convert units: 7.4 kWh/m\(^2\) to W/m\(^2\), compare to the solar constant.
- What is the reason for the difference?
- How is this information useful?
Solar thermal
- Key types
- non-concentrated
- e.g., hot water heating
- concentrated
- high temperature, power generation
- non-concentrated
- Focus on concentrated here
- Concentrate solar energy using reflectors
- Higher temperatures for heat engine efficiency
- Energy storage benefits over PV
- Store the existing high T fluid, versus batteries
- Higher
costs than PV
- See also the LCOE chart.


Solar thermal
- Linear recievers:
- Parabolic trough
- oil, molten salt, pressurized steam
- most common
- Enclosed trough
- sheltered from wind, dust
- Fresnel reflector: lower costs
- efficiencies 8-18%
- only need one axis tracking
- Parabolic trough
- Point recievers:
- Power tower
- higher temperatures
- allows uneven ground
- 1st in Spain, 2007, 11 MW
- Largest = Mohammad bin Rashid, UAE, 600 MW.
- 3rd largest is Ivanpah in California, 392 MW.
- About 60 plants that are larger than 50 MW.
- consolidated operations
- Dish
- Stirling engine
- High efficiency
- Engineering issues
- efficiencies 20-40%
- dual axis control needed
- Power tower

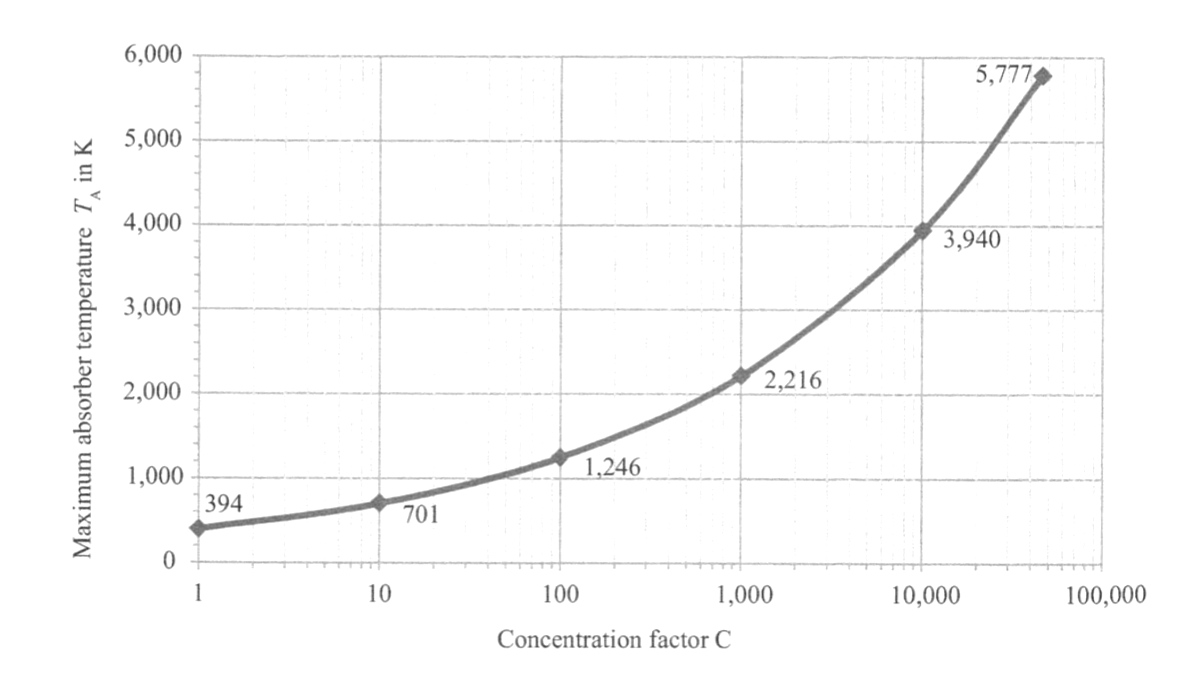
Concentration factor
Question: how much can the sun be concentrated? What are the limits?
Question: what is the maximum temperature a solar reciever can have?
\[C = \frac{A_C}{A_R}\]

Concentration factor
Power (P) emitted from the sun’s surface of radius \(r_S\): \[P_s = \sigma T_s^4 \cdot 4\pi r_s^2\] Power of the sun at solar collector distace \(R_{SE}\) from the sun \[P_c = \sigma T_s^4 \cdot 4\pi r_s^2 \cdot\frac{A_c}{4\pi R_{SE}^2}\] \(\frac{A_c}{4\pi R_{SE}^2}\) is the fraction of power reaching the collector. The best reciever will have power: \[P_r = \sigma T_s^4 A_r\] And \(P_c = P_r\) by conservation of energy. This gives
\[C_\text{max} = \frac{A_c}{A_r} = \frac{R_{SE}^2}{r_s^2} = 46152 \]
Concentration factor
Absorber tubes

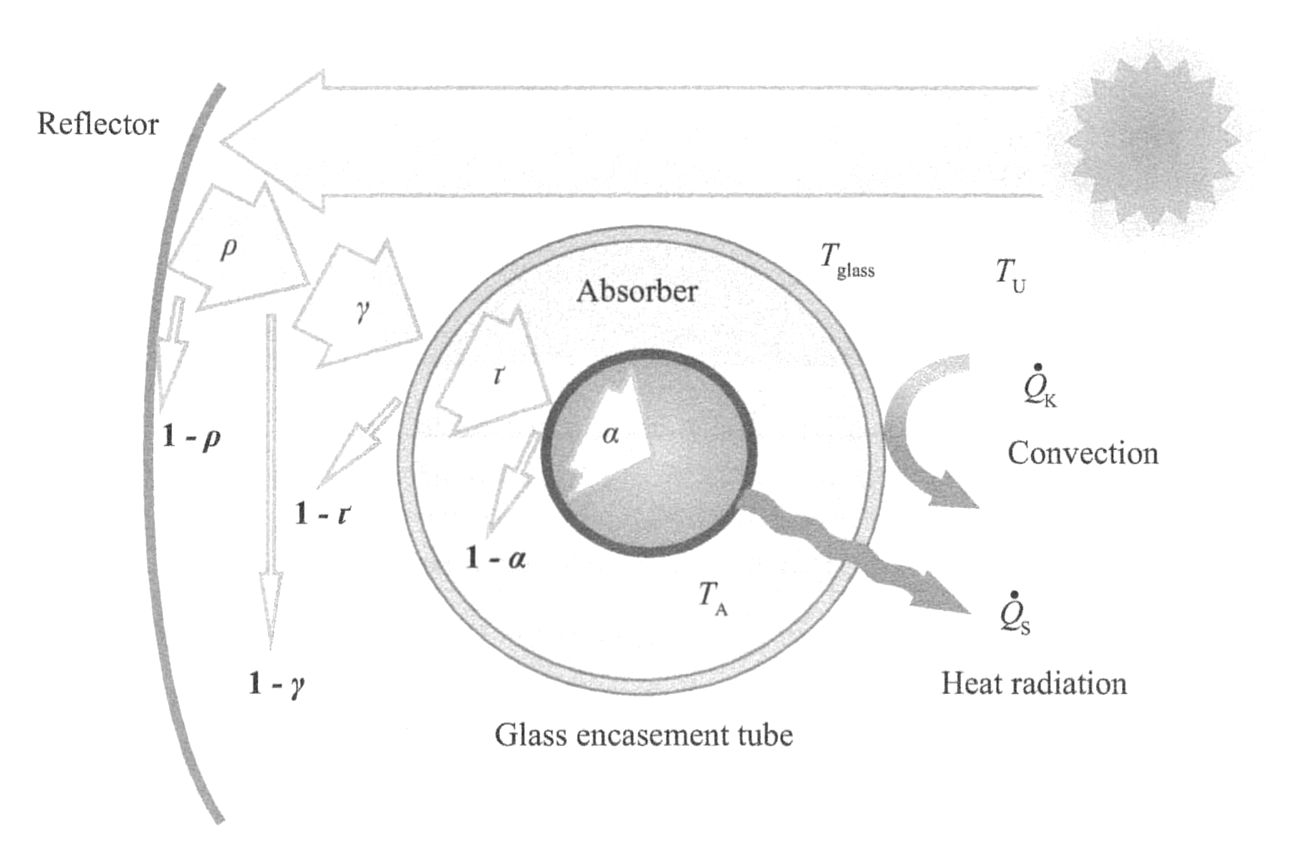
| \(\rho\): reflectivity | \(\gamma\): intercept factor |
| \(\tau\): transmissivity | \(\alpha\): absorptivity |
\[\dot{Q}_S = A_\text{A}\epsilon\sigma(T_\text{A}^4 - T_U^4)\] \[\dot{Q}_K = hA_\text{A}(T_\text{glass} - T_U)\]
Cerro Dominador Plant
- Chile
- 110 MW
- June 2021
- 1.9 GWh energy storage
- molten salt: KNO\(_3\), NaNO\(_3\)
- Up to 17.5 hrs
- Aperature area = 1,484,000 m\(^2\)
- 250 m tower heats salts 560 \(^o\)C
- 100 MW PV component

Photovoltaic effect
- Atomic energy levels are quantized
- Photon (light) energy \(E=hc/\lambda\)
- 13.59 eV (91 nm) light (UV) ionizes hydrogen
- external photovoltaic effect
- Lower energies \(\rightarrow\) internal PV effect
- 13.59 eV (91 nm) light (UV) ionizes hydrogen
- Molecules, atoms, solids \(\rightarrow\) many energies \(\rightarrow\) bands
- electrons occupy the lower bands, and are excited into upper bands

![]()
Conductors, semi-conductors, insulators
Visible light \(\lesssim\) 3 eV

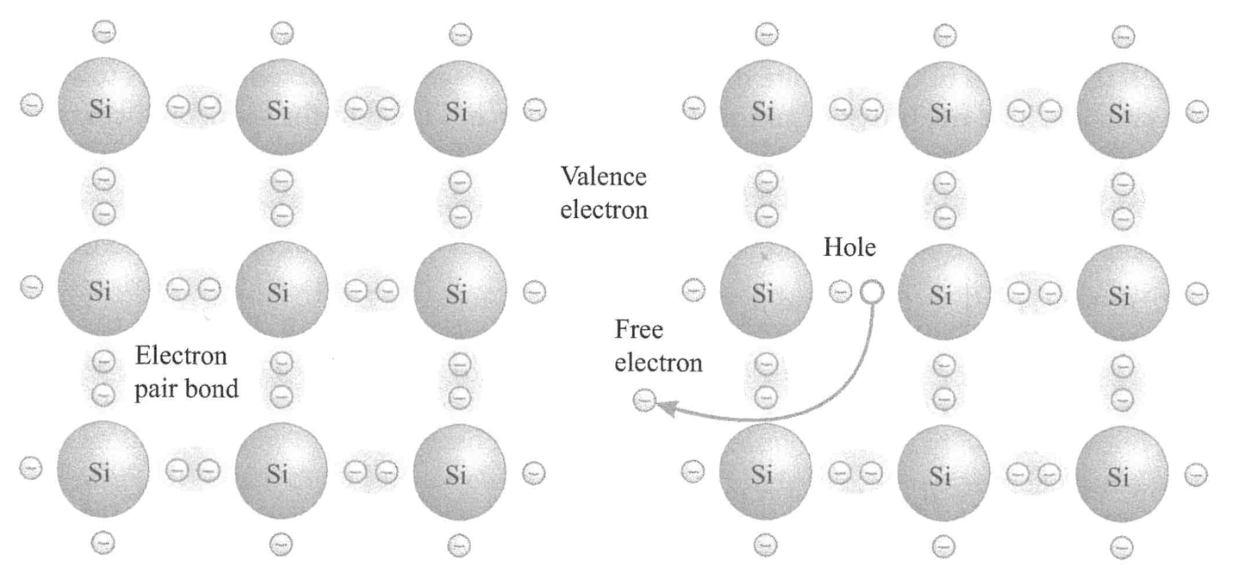
Semiconductors
- PV cells use semi-conductors
- Group IV elements: Si, Ge, Sn; 4 valence electrons \(\rightarrow\) in the crystal shared
electrons in covalent bonds fill the valence band.
- Light can raise electrons to the conduction band: free electron + a hole
- Groups III + V, II+VI
Semiconductors
- PV cells use semi-conductors
- Group IV elements: Si, Ge, Sn; 4 valence electrons \(\rightarrow\) in the crystal shared
electrons in covalent bonds fill the valence band.
- Light can raise electrons to the conduction band: free electron + a hole
- Groups III + V, II+VI
![]()
p,n Doping
- n electrons, p holes; \(n=p\)
- \(n\cdot p\) is the intrinsic carrier density.
- n-Doping
- replace some Si with Group V elements like phosphorus (P) or antimony (Sb)
- five valence electrons \(\rightarrow\) one left over, weakly bound
- more free electrons than holes; electrons are the majority carriers
- p-Doping
- replace some Si with Group III elements like Boron (B) or aluminum (Al)
- three valence electrons \(\rightarrow\) one missing
- holes are the majority carriers
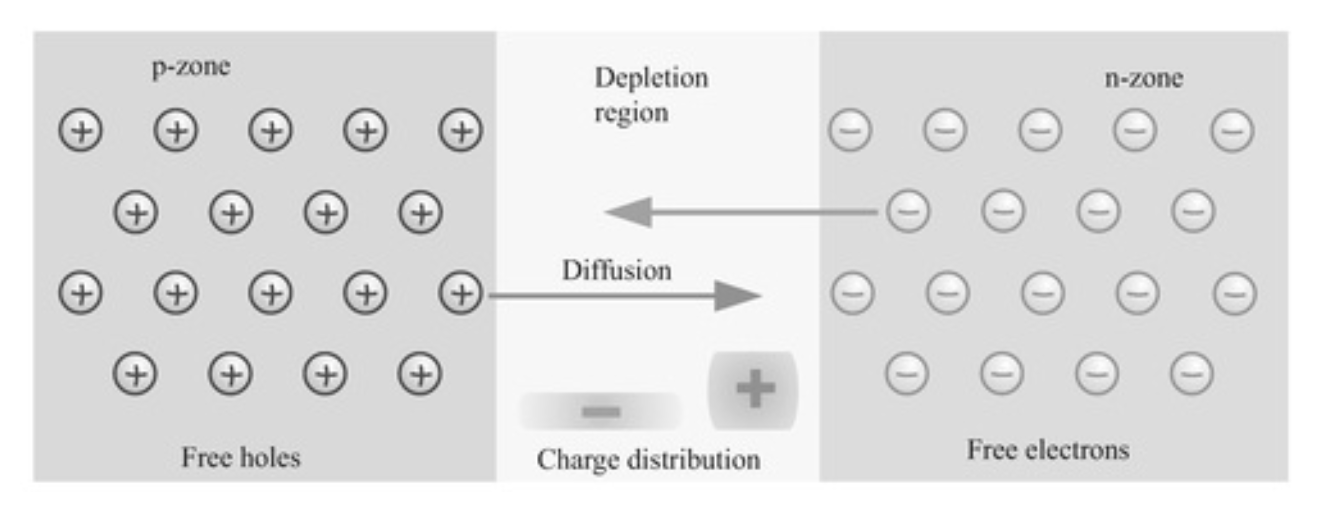
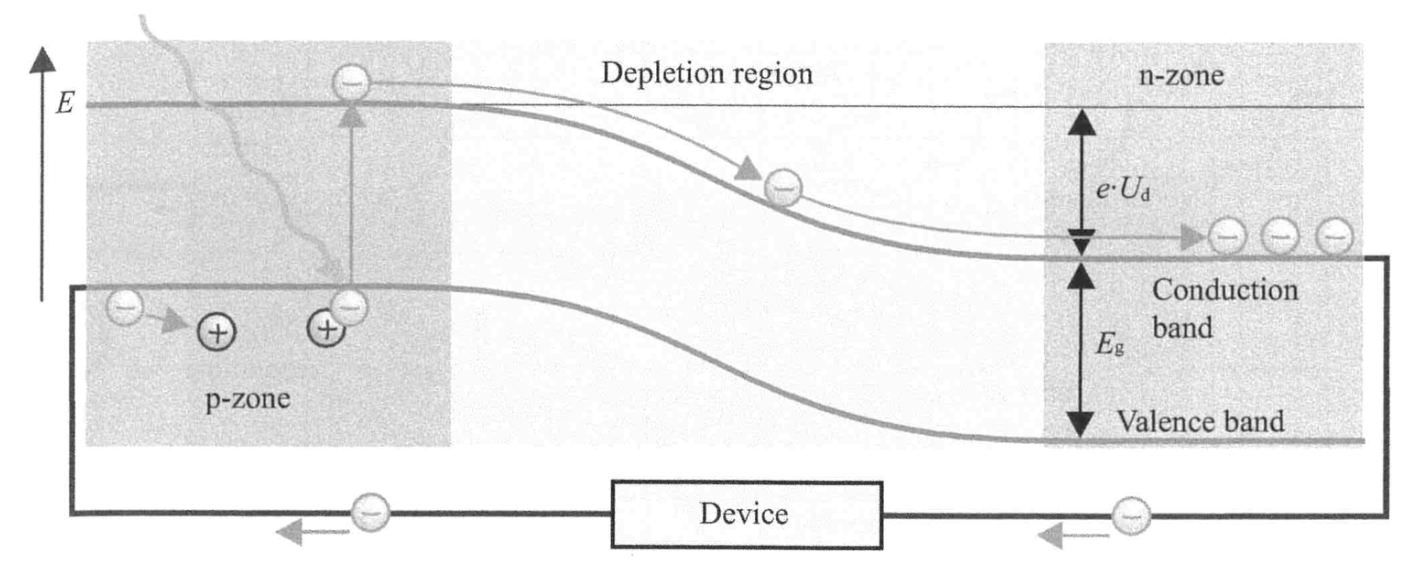
- p-n junction:
- electrons move from the n-region to the p-region, and vice-versa for the holes
- an electric field is formed that opposes continued motion
- voltage ~0.5 V open circuit silicon single junction
p-n Junction
Video
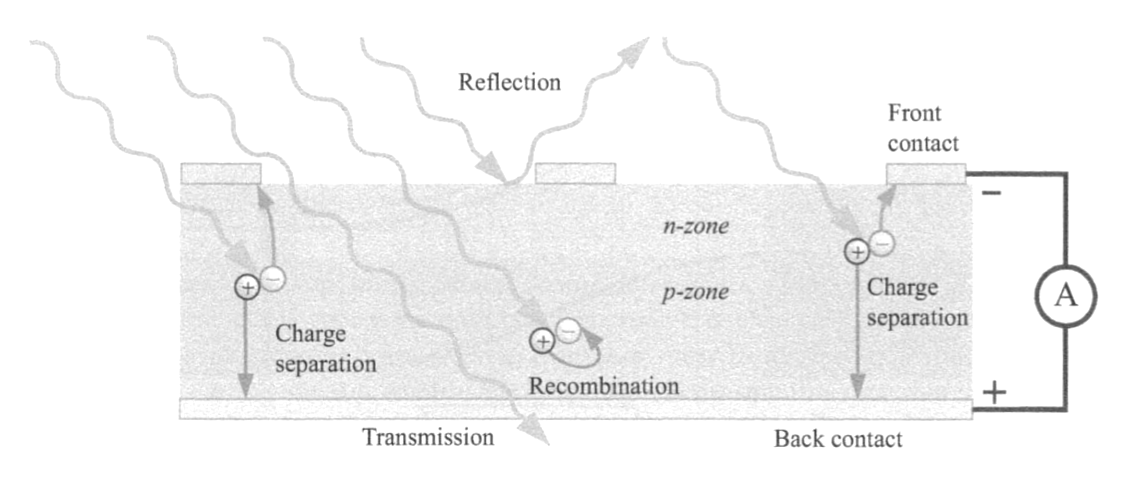
Losses
- Shading
- Transmission
- Reflection
- Absorption
- Heat losses
- photons energy > band gap lost to heat
Efficiency
\[\eta = \frac{\text{electrical power}}{\text{incident solar power}}\]
- Shockley-Queisser
limit:
- \(\eta\) = 33%
- single p-n junction
- Multiple junctions
- differing band gaps optimize to different parts of the spectrum
Efficiency

Video
Solar panel
- Series arrangment
- 0.5 V \(\cdot\) 36 = 18 V
- ~17% efficient
- 25-30 years
- textured surfaces