ChEn 433 Wind

Class 19-20

Wind

What are the major issues associated with wind power?

  • Intermittent wind
    • energy storage
  • Location of wind vs population centers
  • Large land use
  • Visual impacts
  • Birds
  • Lifetime, landfill

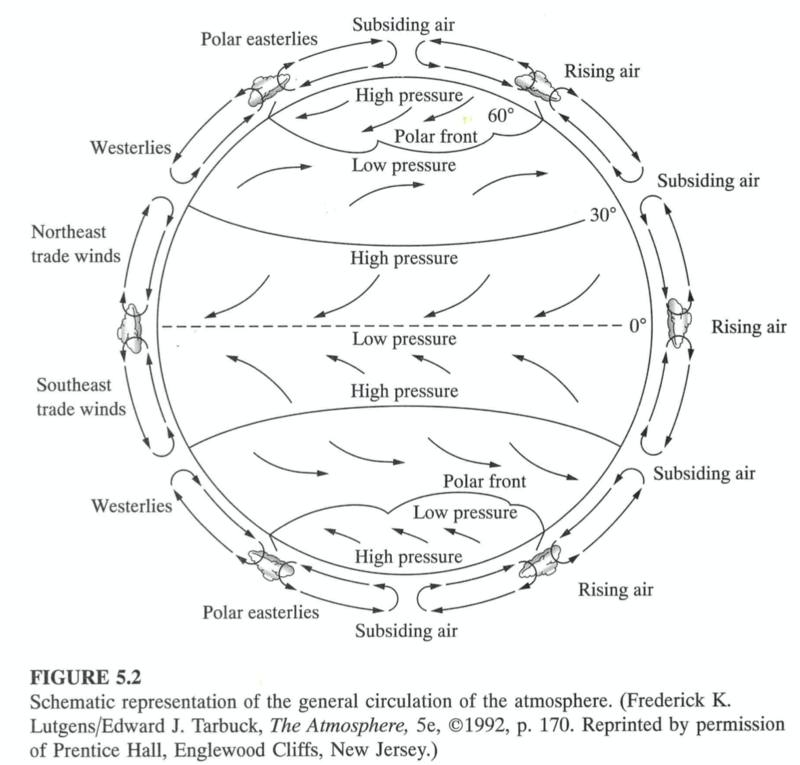
Wind, global

  • Warm air rises at the equator
  • Cold air sinks at the poles
  • Three cells in each hemisphere
  • Atmosphere is thin
    • 50% of mass within 3.4 miles
    • 99% of mass within 20 miles
    • \(D_\text{earth}\approx\) 8000 miles
    • \(\rightarrow\) 2D flow

Wind–Coriolis

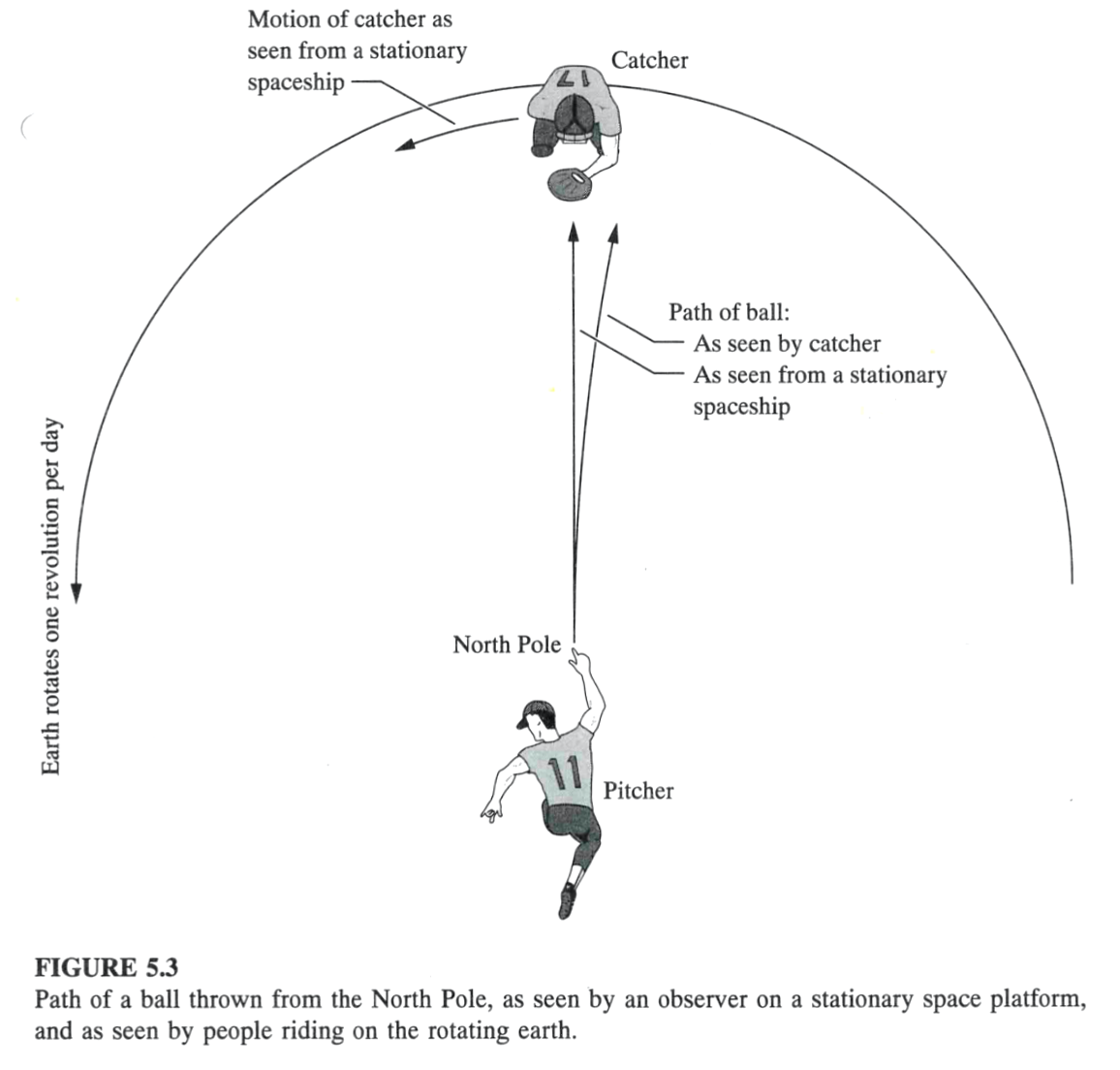
Wind–Coriolis

  • Coriolis acceleration \[a_c = 2v\omega\sin\phi_\text{lat}\]
    • \(\omega = 2\pi\) rad/day = \(7.27\times 10^{-5}\) rad/s
    • at \(\omega = 40^o\) latitude (Provo), v=10 mph:
    \[a_c=\text{2.85E-4 m/s}^2\]
    • \(\ll\) smaller than gravity (ignore for vertical motions)
  • Typical horizontal P gradient = 1 Pa/km. \[a = \frac{F}{m} = \frac{A\Delta P}{\rho V} = \frac{x^2\Delta P}{\rho x^3} = \frac{\Delta P}{\rho x}\] \[a = \text{8.3E-4 m/s}^2\approx 3a_c\]

Wind–height

  • horizontal \(\nabla P\) are ~ const. with height
  • \(\rho\) decreases with height
  • So, \(a\) increases with height, hence v
  • Friction boundary layer \(\lesssim\) 500 m
    • geostrophic wind above this
  • Velocity increase with height \[v = v_0\left(\frac{h}{h_0}\right)^{1/7}\]
    • Hellmann potential
    • (and turbine power increases as \(v^3\))

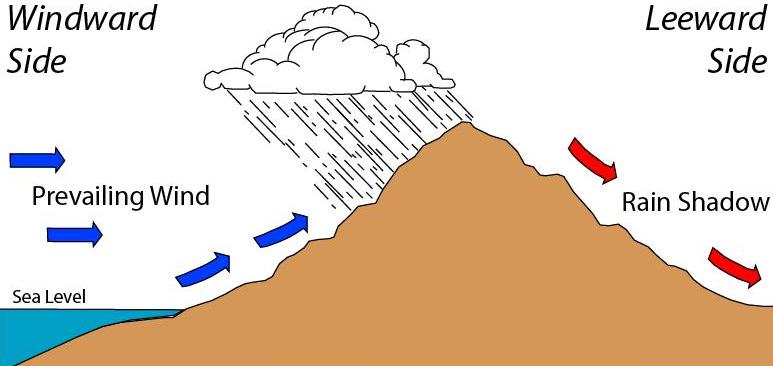
Wind–ground effects

  • Mountains
  • Valleys
  • Land versus water
  • Sea/land breezes
  • Day/night temperature changes
  • Monsoon
    • hot land, draws in moist air from oceans
    • rises, cools, condense to rain

Rain shadow

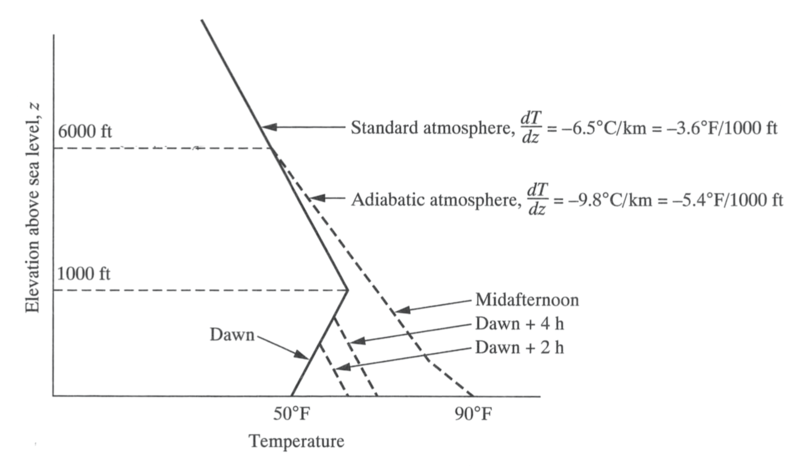
Temperature inversion

  • Daily temperature inversion
    • Surface cools at night
    • Cools surrounding air
    • Slowly reverts during the day
  • Inversion \(\rightarrow\) stable air
    • Morning: hot air balloons
    • Afternoon: soaring birds
      • updrafts, dust devils

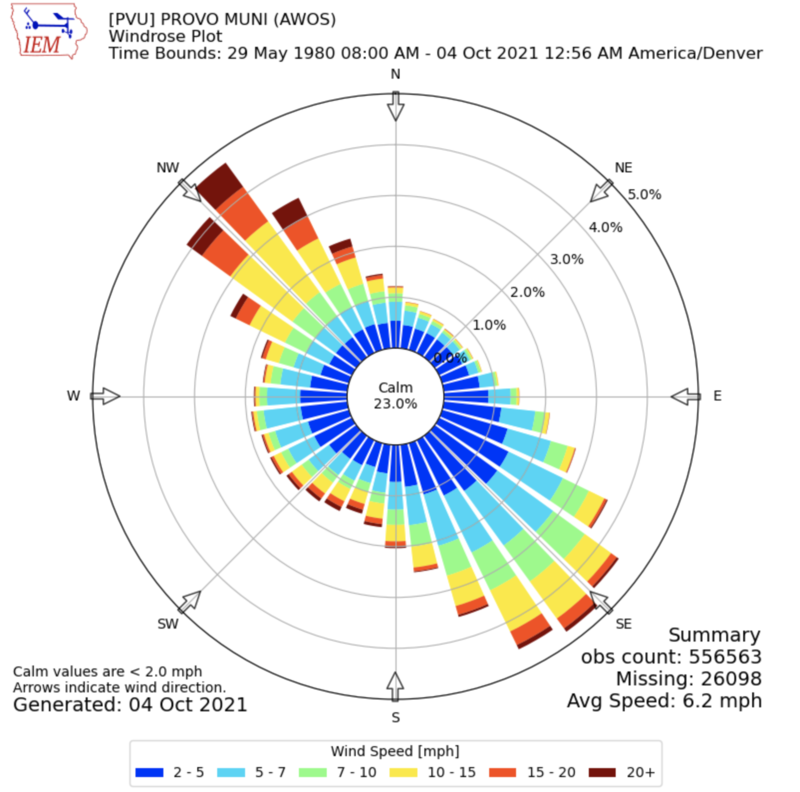
Typical Wind Speeds ~ 10 mi/h ~ 4.5 m/s


Wind direction is the direction the wind is coming from
Wind speed typically measured at a height of 10 m

Wind Rose

Wind classification

Bg v (m/s) v (mph) Designation Effect
0 0–0.2 0-0.45 No wind Smoke rises straight up
1 0.3–1.5 0.67-3.4 Light air Wind direction only detectable from smoke
2 1.6–3.3 3.6-7.4 Light breeze Palpable wind, leaves rustle
3 3.4–5.4 7.6-12 Gentle breeze Leaves and thin twigs move
4 5.5–7.9 12.3-17.7 Moderate breeze Wind moves twigs and thin branches, carries dust
5 8.0–10.7 17.9-24 Fresh breeze Small trees begin to sway
6 10.8–13.8 24.2-30.9 Strong breeze Thick branches move, wind begins to whistle
7 13.9–17.1 31.1-38.2 Near gale Trees in motion, hard to walk
8 17.2–20.7 38.5-46,3 Fresh gale Twigs broken off trees
9 20.8–24.4 46.5-54.6 Strong gale Minor damage to buildings and roofs
10 24.5–28.4 54.8-63.5 Whole gale Trees uprooted
11 28.5–32.6 63.7-72.9 Violent storm Heavy damage
12 ≥ 32.7 ≥ 73.1 Hurricane force Severe damage

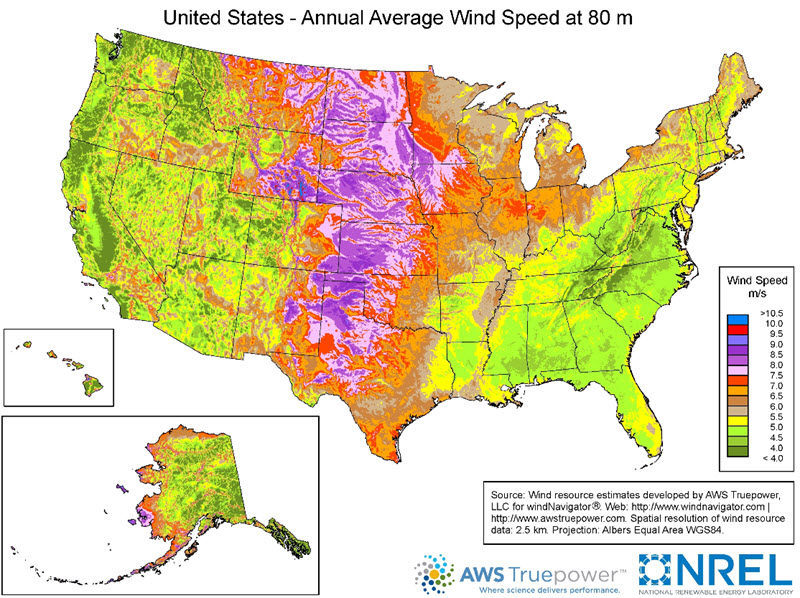
US wind map

Transmission (article)

US wind by state

Interactive map

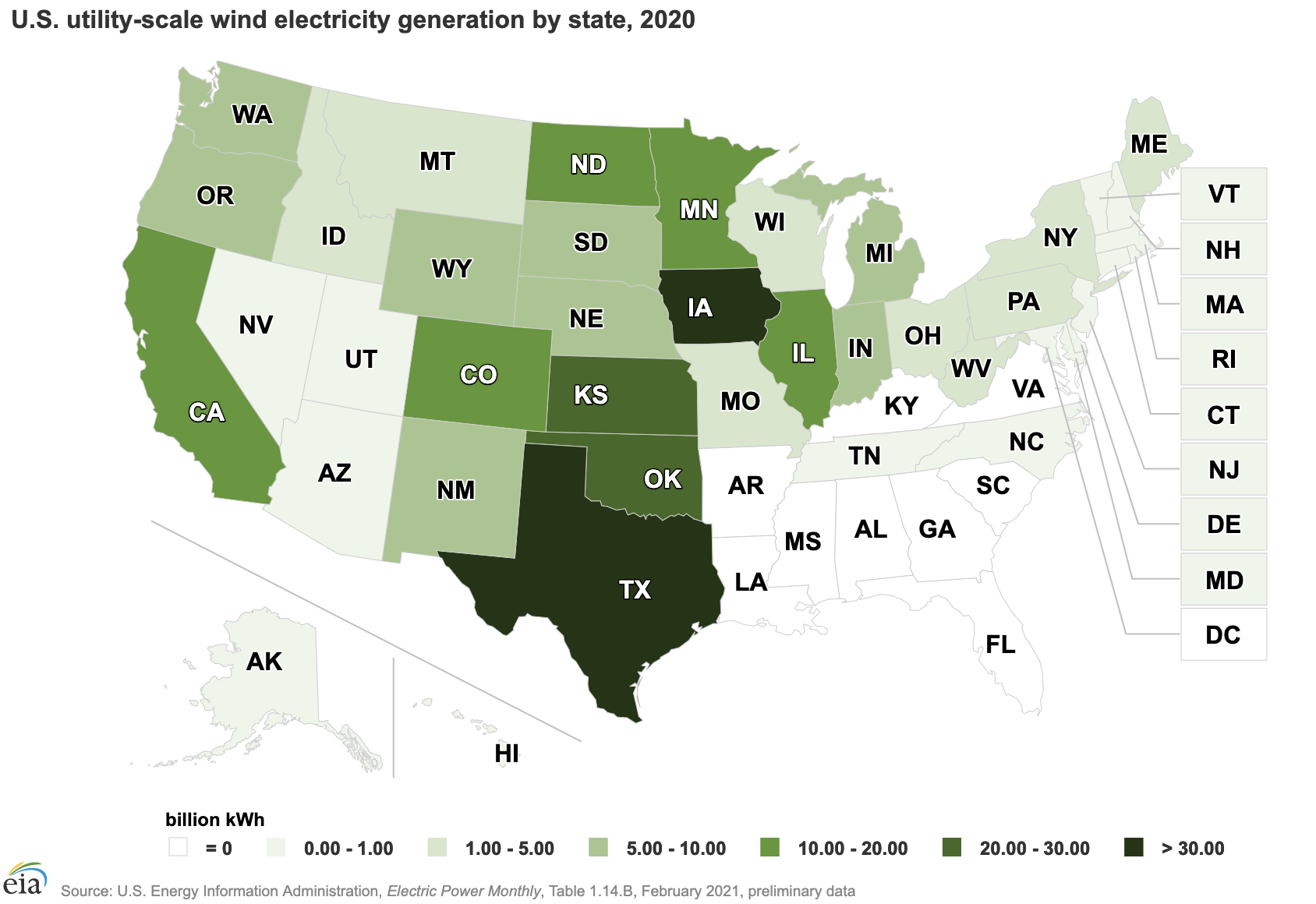
US installed wind capacity by state

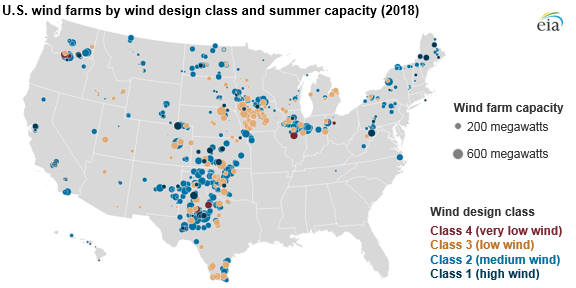
US wind farms

World Wind Energy

Capacity

Generation

1400 TWh/yr = 160 GW

A sense of scale: 1 CMO of Wind Turbines

  • 2,478,571 average sized land-based wind turbines
    • Build 953 per week for 50 years
    • 2 MW (typical)
    • 8751 average size land-based wind farms
      • 566 MW each (the avg size above 250 MW)
      • 283 turbines each at 1.65 MW
      • Build 5 farms a week for 33 years
    • Using a 35% capacity factor.


3 CMO for typical wind farm area

Turbine types

  • Drag turbines
    • higher drag on one side \(\rightarrow\) spin
    • simple
    • max \(C_p=0.19\)
  • Lift turbines
    • faster speeds
    • less material
    • higher max \(C_p=0.59\)

   

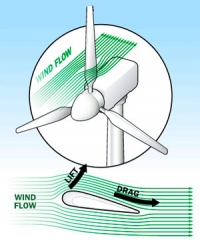
Turbine types – HAWT

Turbine types – VAWT

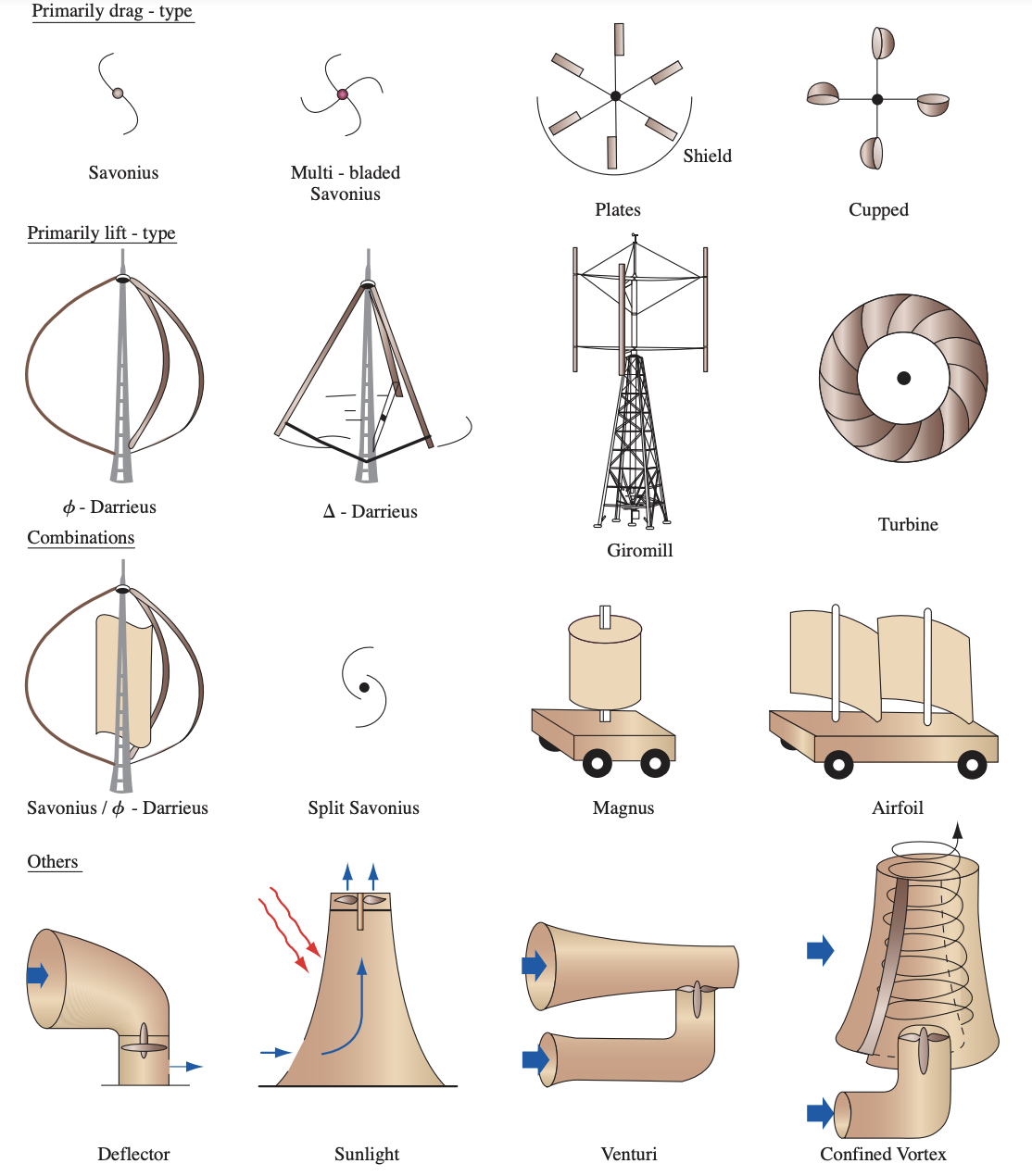
Turbine types – VAWT

  • Benefits
    • Relatively simple structures
    • generator, gearbox, electrical controls can be stored in the ground station.
      • easier to maintain
    • do not have to track the wind
      • good for regions where the wind direction changes quickly
  • Detriments
    • Lower efficiency compared to HAWT
    • material fatigue due to frequently changing loads.
    • more material.
  • Used in specialized applications, where certain noted benefits are desired.

Turbine types – VAWT

  • Savonius
    • \(C_{p,\text{max}}\) = 0.25
    • overlap \(\rightarrow\) some lift
    • startup at low wind speeds \(\rightarrow\) ventilation
    • material intensive
    • used to startup Darrieus rotors
  • Darrieus
    • lift turbine.
    • blade angle changes in the wind as it rotates
    • more efficient than Savonius, 75% as efficient as HAWT.
    • not self-starting.
    • H-rotor version
      • extreme weather conditions, very robust

Turbine components

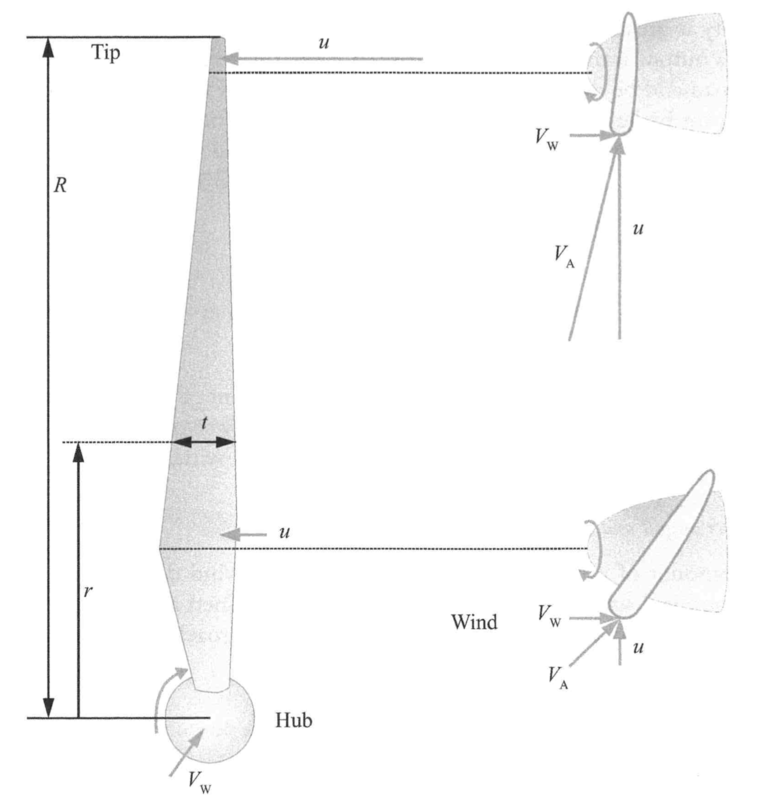
Turbine blades

Turbine video

Typical turbine

  • Vestas V90
    • 2 MW
    • 44 m blades, 90 m rotor diameter
      • 6362 m\(^2\) swept area
    • 80 m tower height
    • Noise: 104 dB (~helicopter, lawnmower)
    • wind speeds: 4-25 m/s (9-56 mph)
  • Blade tip speeds
    • 167 mph for a 90 m diameter turbine

Wind turbine analysis

  • Ideal analysis
    • No frictional losses
    • Bernoulli equation holds
    • one-dimensional flow
  • Power is \(\dot{m}\) times change in KE \[\dot{W}= \frac{1}{2}\dot{m}(v_1^2 - v_4^2)\]
  • Now, \(\dot{m}\) is given by \[\dot{m}=\rho Av\]
    • A is area swept by rotor
    • v is the velocity at the rotor
  • v is unknown, calculate it

\(A\) = circular area swept by the rotor

Wind turbine analysis

Momentum balance: 1 \(\leftrightarrow\) 4 \[\cancel{\dot{\text{accum}}} = \dot{\text{in}} + \dot{\text{out}} + \dot{\text{gen}}\] \[0 = \dot{m}v_1 - \dot{m}v_4 - F\]

Momentum balance: 2 \(\leftrightarrow\) 3 \[0 = \cancelto{\,0,\,v_2=v_3}{\dot{m}v_2 - \dot{m}v_3} +P_2A-P_3A - F\]

Combine these: \[\dot{m}(v_1-v_4) = A(P_2-P_3) = F\]

\(A\) = circular area swept by the rotor

Wind turbine analysis

Again: \(\dot{m}(v_1-v_4) = A(P_2-P_3) = F\)

Write \(P_2\) in terms of \(P_1\) using Bernoulli Eq. \[\frac{P_2}{\rho} + \frac{v_2^2}{2} = \frac{P_1}{\rho} + \frac{v_1^2}{2}\] \[P_2 = P_1 + \frac{\rho v_1^2}{2} - \frac{\rho v_2^2}{2}\]

Similarly for \(P_3\) in terms of \(P_4\) \[P_3 = P_4 + \frac{\rho v_4^2}{2} - \frac{\rho v_3^2}{2}\]

Now, insert these into \(\dot{m}(v_1-v_4) = A(P_2-P_3)\)

Wind turbine analysis

\[\frac{\rho A}{2}(v_1^2 - v_4^2) = \dot{m}(v_1-v_4)\]

Let \(v=v_2=v_3\) with \(\dot{m}=\rho Av\). This gives \[v = \frac{1}{2}(v_1+v_4)\]

Now, power is \(\dot{m}\) times change in KE: \[\dot{W}= \frac{1}{2}\dot{m}(v_1^2 - v_4^2) = \frac{1}{4}\rho A(v_1+v_4)(v_1^2-v_4^2)\]

  • Competition: \(\dot{m}\), \(\Delta KE\)
    • \(\Delta KE \uparrow \text{ with } \downarrow v_4\), but
    • \(\dot{m} \downarrow \text{ with } \downarrow v_4\)

Wind turbine analysis

  • Find the max power for given wind speed \(v_1\).
  • Solve for \(v_4\) where \(d\dot{W}/dv_4=0\). \[v_{4,\text{max}}=\frac{v_1}{3}\]
  • Insert in \(\dot{W}\) expression: \[\dot{W}_\text{max} = \frac{8}{27}\rho Av_1^3\]

Wind turbine analysis

\[\dot{W}_\text{max} = \frac{8}{27}\rho Av_1^3\]

The “available” power of the air is \[\dot{W}_\text{avail} = \frac{1}{2}\dot{m}v_1^2 = \frac{1}{2}\rho Av_1^3\]

\[C_p = \frac{\dot{W}}{\dot{W}_\text{avail}}\]

\[C_{p,\text{max}} = \frac{16}{27} = 0.5926 \text{ is the Betz number}\] \[\eta = \frac{C_p}{C_{p,\text{max}}}\]


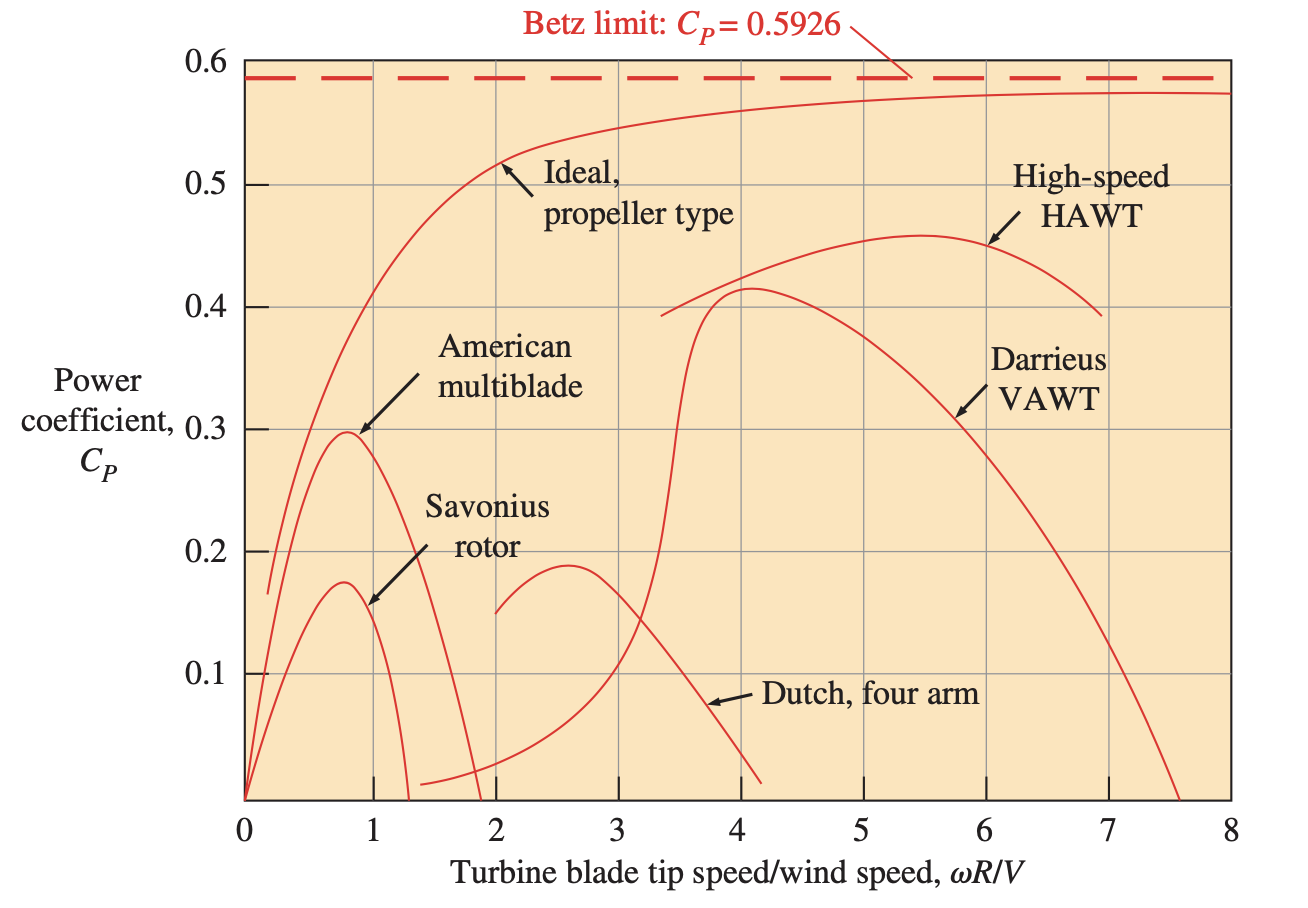
\(\omega R/V = \lambda\) is common notation

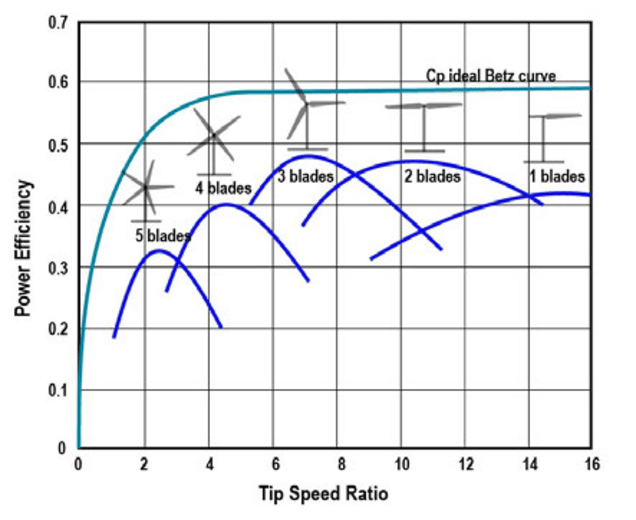
Number of blades

See also: link.

Number of blades

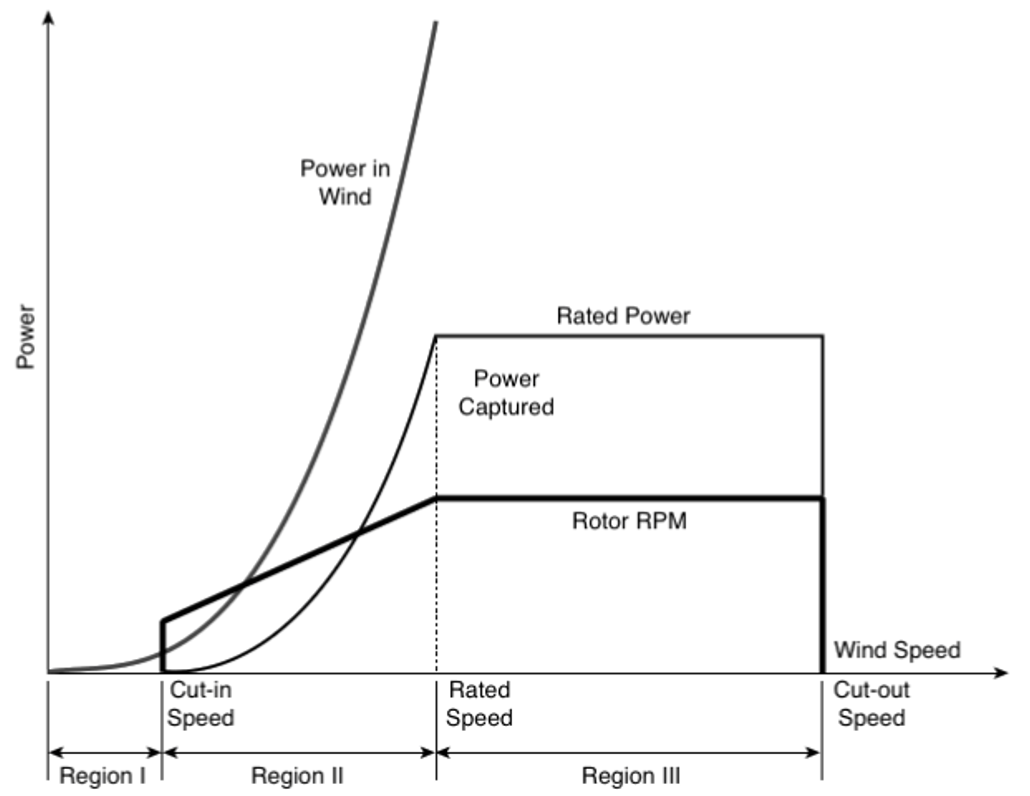
Power curve

Wind Farms

San Gorgonio Pass, CA

Wind farm simulation

Wind farm fog

Wake turbulence behind individual wind turbines can be seen in the fog in this aerial photo of the Horns Rev wind farm off the Western coast of Denmark. Data collected from wind farms such as this one provide validation to simulation models.