ChEn 433 Combustion
David Lignell
Class 8
Combustion
What is combustion?
- What is combustion?
- How can we define it?
- What are its properties and characteristics?
- How do we know something is combustion and when it is not?
Definitions from the web

Webster’s
Rapid oxidation generating heat, or both light and heat; also, slow oxidation accompanied by relatively little heat and no light

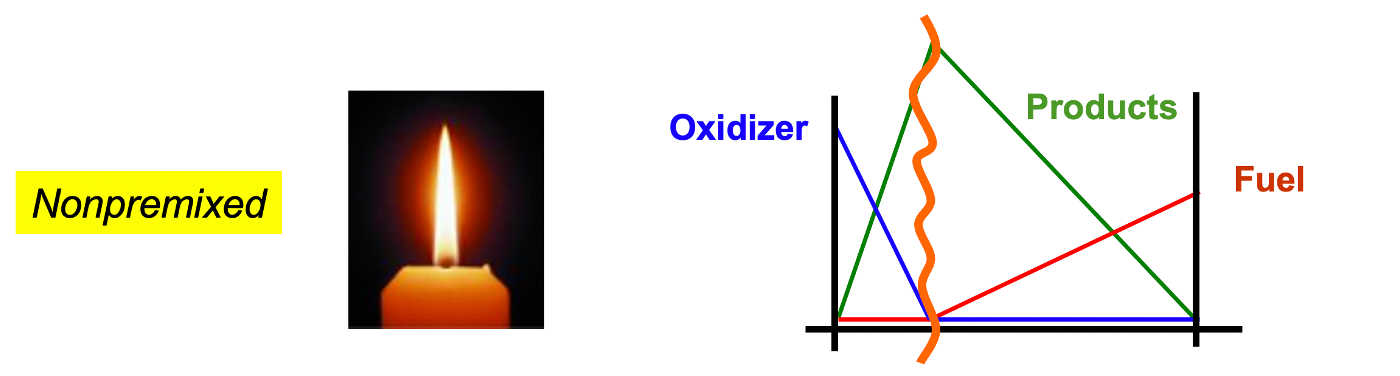
Premixed and nonpremixed
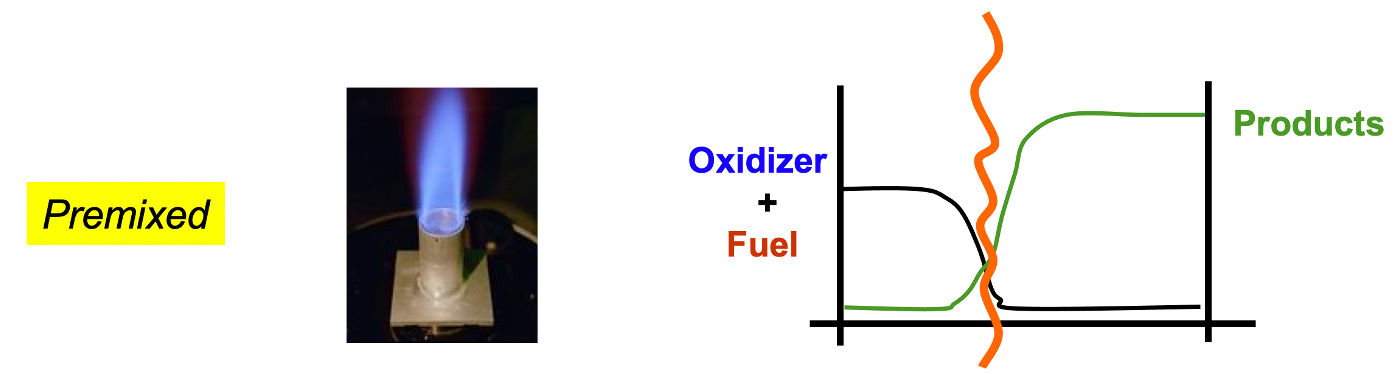
Premixed and nonpremixed

Air properties
Use \(x\) for mole fraction, \(y\) for mass fraction.
Lump Ar with N\(_2\)
n\(_{N2}\)/n\(_{O2}\) = 3.76
n\(_{air}\)/n\(_{O2}\) = 4.76
| species | x | y |
|---|---|---|
| N\(_2\) | 0.7809 | 0.75532 |
| O\(_2\) | 0.2095 | 0.23144 |
| Ar | 0.0096 | 0.01324 |
| species | x | y |
|---|---|---|
| N\(_2\) | 0.79 | 0.77 |
| O\(_2\) | 0.21 | 0.23 |
MW, x-y conversions
M\(_{air}\) = 29 kg/kmol
\[ M = \sum_k x_k M_k,\] \[ M = \frac{1}{\sum_k \frac{y_k}{M_k}}.\]
Convert \(x_k\) to \(y_k\)
\[ x_kM_k = y_kM,\] \[ y_k = \frac{x_kM_k}{M},\] \[ x_k = \frac{y_kM}{M_k}.\]
Stoichiometry
- Rich (too much fuel)
- Lean (too much air)
- Stoichiometric (Goldilocks)
Air-to-Fuel Ratio \[\frac{A}{F} = \frac{m_{air}}{m_{fuel}}\] \[0\le A/F\le\infty\]
Equivalence Ratio
\[\phi = \frac{F/A}{(F/A)_{stoic}}\] mass or mole basis is same
\[0\le\phi\le\infty\]
\(\phi<0\) is lean
\(\phi > 1\) is rich
common in applications
Mixture fraction
\[\xi = \frac{m_f}{m_f + m_a}\]
\[0\le\xi\le 1\]
Like a mass fraction
\(\xi=0\) is pure air
\(\xi=1\) is pure fuel
common in modeling
Balanced reactions
Write the stoichiometric reaction for methane combustion
- 1 mole fuel basis (typical)
- products: \(C\rightarrow CO_2\), \(H\rightarrow H_2O\)
- Solve for species coefficients by balancing elements
\[CH_4 + 2(O_2 + 3.76N_2) \rightarrow CO_2 + 2H_2O + 7.52N_2\]
What is \(m_f/m_a\)?
\[m_f/m_a = M_{CH4} / (2*4.76*M_{air}) = 16/(9.52*29) = 0.058\]
5.8% of mass is fuel.
Generalize the fuel
Try out \(C_xH_y\)
\[C_xH_y + \left(x + \frac{y}{4}\right)O_2 + 3.76\left(x+\frac{y}{4}\right)N_2 \rightarrow xCO_2 + \frac{y}{2}H_2O + 3.76\left(x+\frac{y}{4}\right)N_2\]
Rich and Lean
\[C_xH_y + \left(x + \frac{y}{4}\right) + 3.76\left(x+\frac{y}{4}\right)N_2 \rightarrow xCO_2 + \frac{y}{2}H_2O + 3.76\left(x+\frac{y}{4}\right)N_2\]
Rich
Write the rich reaction in terms of \(\phi\)
\[\phi C_xH_y + \left(x+\frac{y}{4}\right)O_2 + 3.76\left(x+\frac{y}{4}\right)N_2 \rightarrow xCO_2 + \frac{y}{2}H_2O + 3.76\left(x+\frac{y}{4}\right)N_2 + (\phi-1)C_xH_y\]
Lean
Write the lean reaction in terms of the fractional excess air \(E\)
\[C_xH_y + (1+E)\left(x+\frac{y}{4}\right)(O_2 + 3.76 N_2) \rightarrow xCO_2 + \frac{y}{2}H_2O + E\left(x+\frac{y}{4}\right)O_2 + (1+E)3.76\left(x+\frac{y}{4}\right)N_2\]
Flame temperatures
What is the temperature of a flame?

Flame temperatures

- heat loss
- flame strain
- fuel/oxidizer composition
- local stoichiomtry
- …
Adiabatic flame temperature
- No heat losses
- Typically computed as a thermodynamic property, independent of flow physics
Formulate a relation to allow calculation of \(T_{ad}\)
Adiabatic \(\rightarrow\) \(h_\text{reactants} = h_\text{products}\)
\[h = h(T, y_i)\] \[h = \underbrace{h_f(T_\text{ref}, y_i)}_{\sum_iy_ih_{f,i}(T_\text{ref})} + \int_{T_\text{ref}}^T\underbrace{c_p(T,y_i)}_{\sum_iy_ic_{p,i}(T)}dT\]
Then, \(h_\text{reactants} = h_\text{products}\) is one equation in one unknown \(T_\text{products}\equiv T_{ad}\)
\(c_{p,i}(T)\) is typically given as a polynomial in \(T\), in two temperature ranges
Flame temperatures
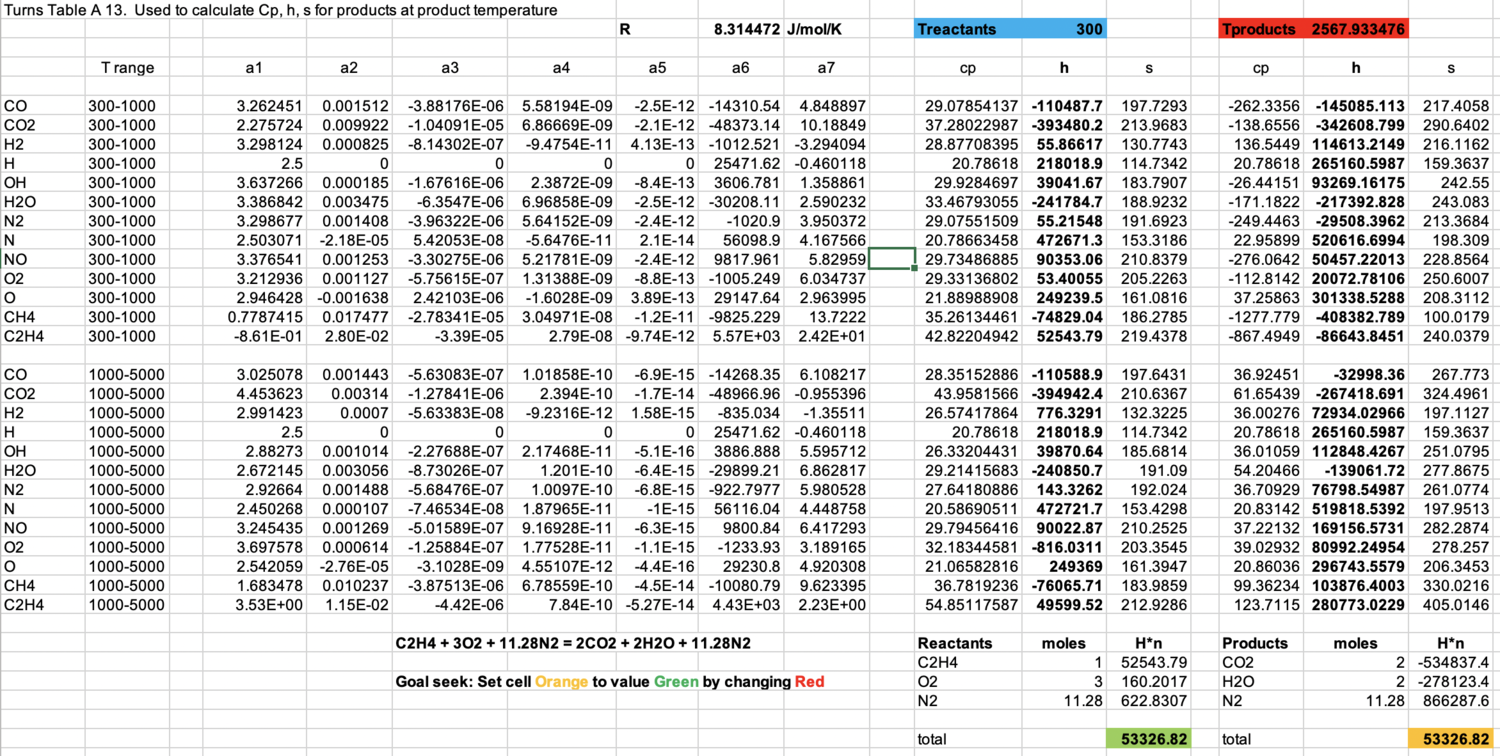
Flame expansion