ChEn 433 Steam

David Lignell

Class 7

Rankine cycle

  • Key power generation cycle: coal, nuclear, natural gas, etc.
  • Heat input from a heat source: combustion, nuclear, geothermal, solar.
  • Heat rejection: river, ocean, lake, atmosphere (dry cooling).
  • Water is used as the working fluid.
    • available
    • non-toxic, non-hazardous, non-reactive
    • pump liquid, phase change gives \(Q_{isoT}\)

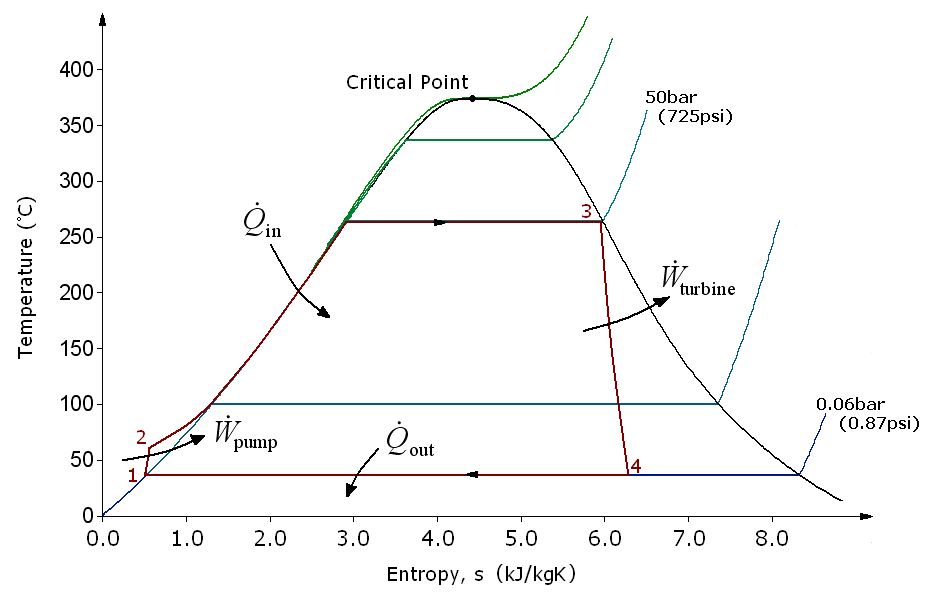
Rankine cycle

  • 1-2: \(W_{in}\), pump liquid from low P to high P; isentropic compression
  • 2-3: \(Q_{in}\), heat at constant pressure: boiling
  • 3-4: \(W_{out}\), expand fluid through turbine; isentropic expansion
  • 4-1: \(Q_{out}\), cool in condenser; vapor to liquid

Rankine cycle: issues

Issues?

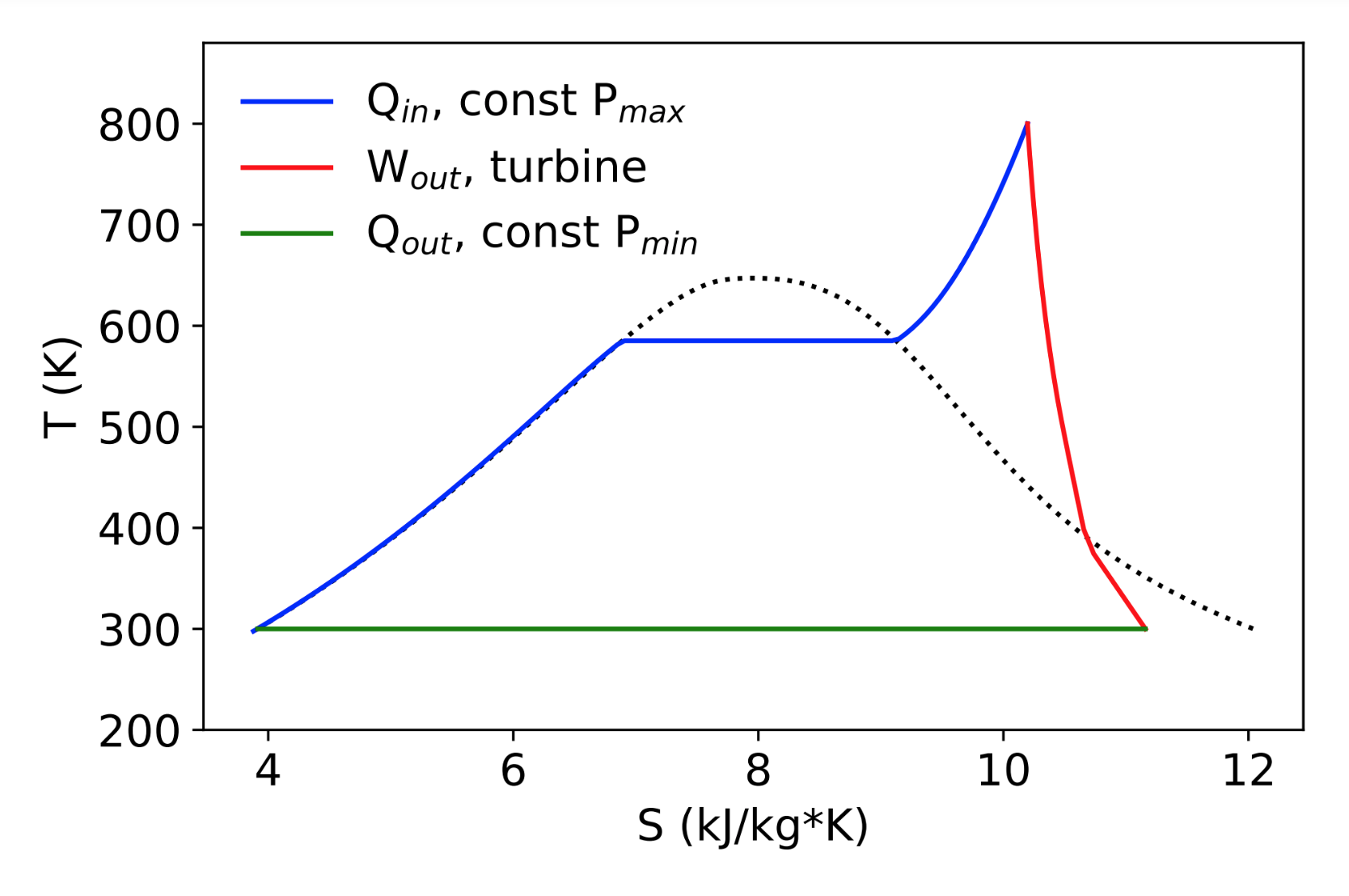
Rankine cycle: TS

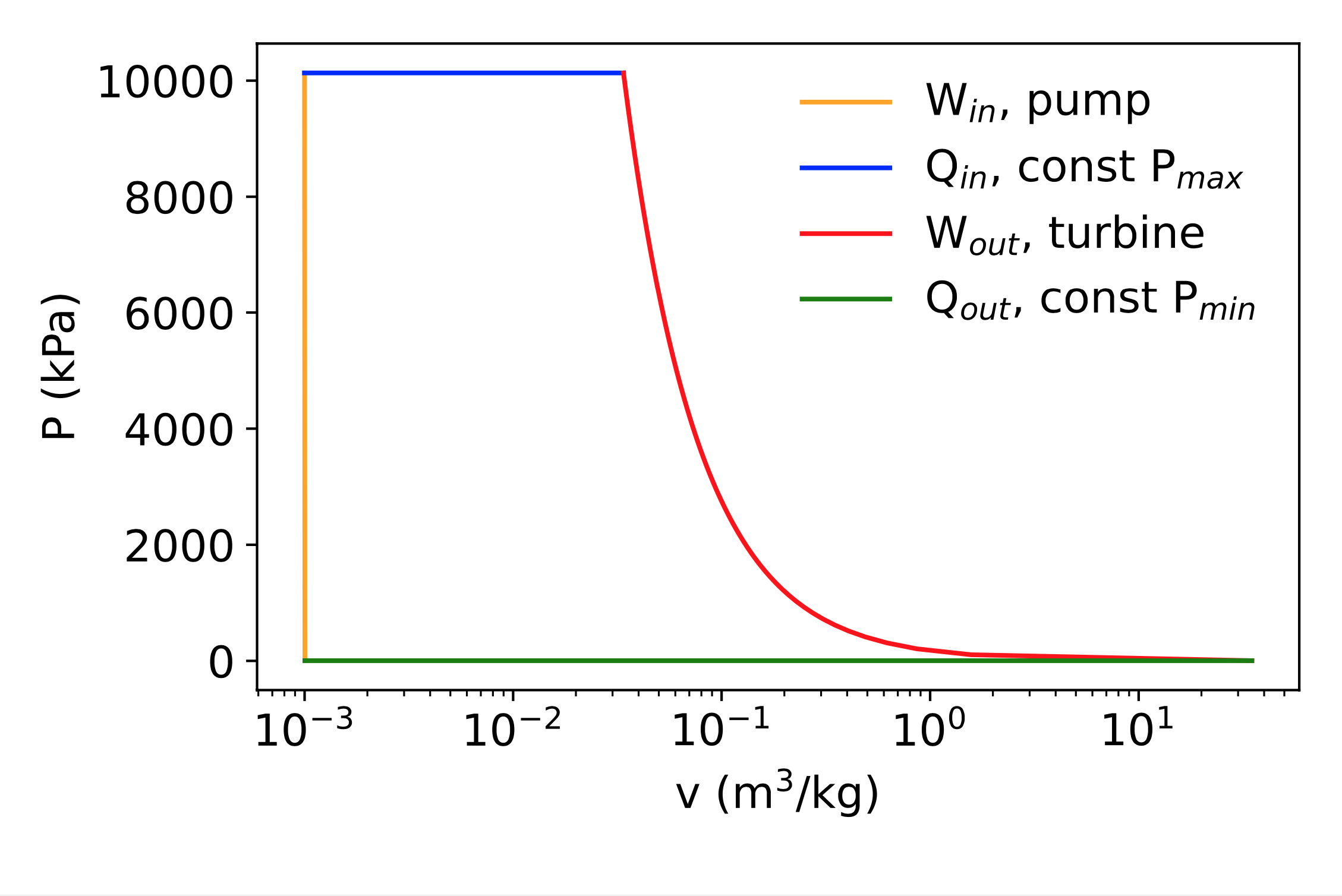
Rankine cycle: PV

What does the PV diagram look like?

Rankine cycle: nonidealities

Nonidealities?

  • Pressure drop in the boiler
  • Nonideal turbine
  • Subcool the condensed liquid to avoid pump cavitation
  • Heat losses to surroundings

Rankine cycle: increase \(η\)

Increase efficiency?

  • Decrease condenser pressure (hence temperature)
    • real condensers operate below atmospheric pressure
    • limited by the saturation pressure corresponding to \(T_{cooling}\).
      • river at 20 \(^oC\) \(→\) P=2312 Pa = 0.023 atm.
      • Typically 2-7 kPa
    • but…quality of steam in turbine, and… air leakage
  • Superheat steam to higher T, even supercritical
    • higher turbine exit steam quality
    • but…limited by material performance and cost: 620 \(^oC\) max.

Rankine cycle: increase \(η\)

Increase efficiency?

  • Increase boiler pressure (\(P_c\)=218 atm)
  • Reheat
    • 4-5% higher efficiency.
    • Usually limited to single reheat stage (except for supercritical plants)
      • A second reheat gives \(Δ η\) about half the initial gain.
      • Avoid superheated turbine exhaust.
    • Optimal reheat pressure ~ 1/4 \(P_{max}\)

Rankine cycle: steam with reheat

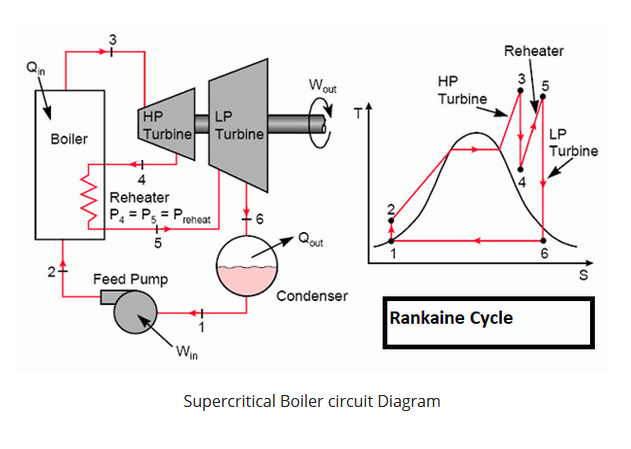
  • 1-2: \(W_{in}\), pump liquid from low P to high P; isentropic compression
  • 2-3: \(Q_{in}\), heat at constant pressure: heat, boil, superheat
  • 3-4: \(W_{out}\), expand fluid through turbine; isentropic expansion
  • 4-5: \(Q_{in}\), re-heat at constant pressure: superheat
  • 5-6: \(W_{out}\), expand fluid through turbine; isentropic expansion
  • 6-1: \(Q_{out}\), cool in condenser; vapor to liquid

Conversion efficiencies

Steam properties: Cantera

Cantera example: steam tables

Cantera example: TS diagram

Cantera example: Rankine cycle

Work potential

  • For conversion of thermal energy to electricity or mechanical work, energy alone is not enough.
    • A 1 K temperature change in the oceans would supply 17000 CMO!
    • But at the average surface temperature, the thermal conversion efficiency would be ~0.003.
  • We really want the work potential of an energy source.
    • Names: exergy, availability, lost work, second law analysis

How much work can be extracted in going from one state to another?

Or, how much work is required in going from one state to another?

Work Potential: KE, PE

The wind blows at 10 m/s, what is the work potential per unit mass?

What is the work potential in a 5.1 meter high waterfall?

Work potential: heat transfer

We transfer 1 kW of power from a thermal energy source at 500 K.

What is the work potential?

Need to define the surrounding state, so, 300 \(K\), say.

WP here is simply 1 kW times the Carnot efficiency: \[W = 1\,\mbox{kW} ⋅ \underbrace{(1 - 300/500)}_{η_c} = 0.40\,\mbox{kW}\]

Work potential: air, change state

Air

quantity state 1 state 2
T (K) 573 300
P (atm) 10 1
S (J/kg\(⋅\)K) 6892 6892
H (kJ/kg) 282 1.91

How much work can be extracted in moving from state 1 to state 2?

Isentropic
Work is just \(Δ H\)
That is, the maximum 1\(^{st}\) law work can be extracted

Work potential: steam, change state

Water

quantity state 1 state 2
Phase supercritical liquid
T (K) 800 300
P (atm) 10 1
S (J/kg\(⋅\)K) 11350 3913
H (kJ/kg) -12434 -15858

How much work can be extracted in moving from state 1 to state 2?

  • First law: \(Δ H = W + Q\)
  • Max work for min Q
  • Second law: \(Q_{min}=T_{min}Δ S\)

Lost work

  • Consider an unsteady, open system
  • Energy balance \[\begin{align} \frac{d(mu)_{sys}}{dt} &= \dot{W} + \dot{Q} + \sum_i\dot{m}_iu_i \\ &=\sum_i\dot{m}_iPv_i + \dot{W}_\phi + \sum_j\dot{Q}_j + \sum_i\dot{m}_iu_i \end{align}\]

Here, \(\dot{W}_\phi\) is “other” work not including injection work (which goes into enthalpy).

\[\frac{d(mu)_{sys}}{dt} = \sum_i\dot{m}_ih_i + \dot{W}_\phi + \sum_j\dot{Q}_j\]

Lost work

  • Entropy balance
    • Here, we define the system so that it exchanges heat with the surrounding reservoirs \(j\) at the respective reservoir temperature. In this way, all irreversibilities are within the system, and \(\dot{S}_{sys} + \dot{S}_{surr} = \dot{S}_{irrev}\). \[\frac{d(ms)_{sys}}{dt} = \sum_i\dot{m}s_i + \underbrace{\sum_j\dot{S}_{j,HT}}_{\sum_j\dot{Q}_j/T_j} + \dot{S}_{irrev}\]

\[\frac{d(ms)_{sys}}{dt} = \sum_i\dot{m}_is_i + \sum_j\dot{Q}_j/T_j + \dot{S}_{irrev}\]

Lost work

  • The term \(\dot{S}_{irrev}\) is identified as the lost work divided by the surrounding temperature \(T_0\): \[\dot{S}_{irrev} = \frac{W_L}{T_0}\]
  • We multiply the entropy balance by \(T_0\) and subtract the result from the energy balance. This gives a relation for the combined first and second laws: \[\frac{d(m(u-T_0s))_{sys}}{dt} = \sum_i\dot{m}_i(h_i-T_0s_i) + \sum_jQ_j\left(1-\frac{T_0}{T_j}\right) + \dot{W}_\phi -\dot{W}_L\]
  • Solve for \(\dot{W}_\phi\): \[\dot{W}_\phi = \left[\frac{d(m(u-T_0s))_{sys}}{dt} - \sum_i\dot{m}_i(h_i-T_0s_i) - \sum_jQ_j\left(1-\frac{T_0}{T_j}\right)\right] + \dot{W}_L\]

Lost work

  • Again: \[\dot{W}_\phi = \frac{d(m(u-T_0s))_{sys}}{dt} - \sum_i\dot{m}_i(h_i-T_0s_i) - \sum_jQ_j\left(1-\frac{T_0}{T_j}\right) + \dot{W}_L\]
  • If the lost work is zero, then we have a reversible process, by which:

\[\dot{W}_{\phi,rev} = \frac{d(m(u-T_0s))_{sys}}{dt} - \sum_i\dot{m}_i(h_i-T_0s_i) - \sum_jQ_j\left(1-\frac{T_0}{T_j}\right)\]

  • \(Q\) is positive into the system
  • \(\dot{m}\) is positive into the system
  • \(\dot{W}_{\phi,rev}\) is positive into the system