ChEn 433 Thermodynamics
David Lignell
Class 5
Energy
- Internal energy
- Only differences matter
- Select a zero state
- Rigorously conserved
- Heat and work are not energy but energy transfer mechanisms
Postulate 1: There exits particular states (called equilibrium states) of simple systems that, macroscopically, are characterized completely by the internal energy \(U\), the volume \(V\), and the mole numbers \(N_1,\,N_2,…\) of the chemical components.
- Time independent
- State retains no time history
In an adiabatic system, the change in energy between two states is the work done on the system.
- Hence, energy changes between two states can be found as the mechanical work done for the adiabatic transition between the states
Heat
\[ΔU = W + Q\]
\[\mbox{Define heat as: }Q≡ ΔU-W\]
\[dW = -PdV\] \[dU = dQ - PdV\]
Central problem of thermodynamics
The single, all-encompassing problem of thermodynamics is the determination of the equilibrium state that eventually results after the removal of internal constraints in a closed, composite system.
Entropy
Postulate 2: There exists a function (called the entropy \(S\)) of the extensive parameters of any composite system, defined for all equilibrium states and having the following property: The values assumed by the extensive parameters in the absence of an internal constraint are those that maximize the entropy over the manifold of contrained equilibrium states.
Fundamental Relation: \[S(U, V, N_i)\] If this fundamental relation (function) is known, all thermodynamic information about the system is known.
Entropy
Postulate 3: The entropy of a composite system is additive over the constituent subsystems. The entropy is continuous and differentiable and is a monotonically increasing function of the energy.
\[S = \sum_α S^{(α)},\] where \(S^{(α)}=S(U^{(α)}, V^{(α)}, N_i^{(α)})\) for some subsystem \(α\).
Entropy
- Additive implies \(S(\lambda U, λV, λN_i) = λS(U, V, N_i)\)
for some constant \(λ\).
- Entropy is a homogeneous, first order function of its parameters.
- Monotonically increasing implies \[\left(\frac{\partial S}{\partial U}\right)_{V,N_i} > 0.\]
- Continuous, differentiable, monotonically
increasing implies \(S(U,V,N_i)\) is invertable to \(U(S,V,N_i)\)
- Then \(U(S,V,N_i)\) is another form of the fundamental relation.
\[dU = TdS - PdV + \sum_iμ_idN_i\]
Reversible processes
- Process occurs through a succession of equilibrium states
- “Slow”
- Reversible
- Frictionless
- Uniform temperature, pressure
- Entropy is conserved
Work from Heat Transfer
With a group, discuss the following questions?
- What is the name of the cycle that maximizes the work from a heat transfer process?
- What did the process look like? Draw a picture. What were the key components?
- How many key steps are there?
- What are the key steps?
- What was the maximum efficiency?
- How is the efficiency defined?
- What key quantity does the efficiency depend on?
- What is its equation?
Carnot Process

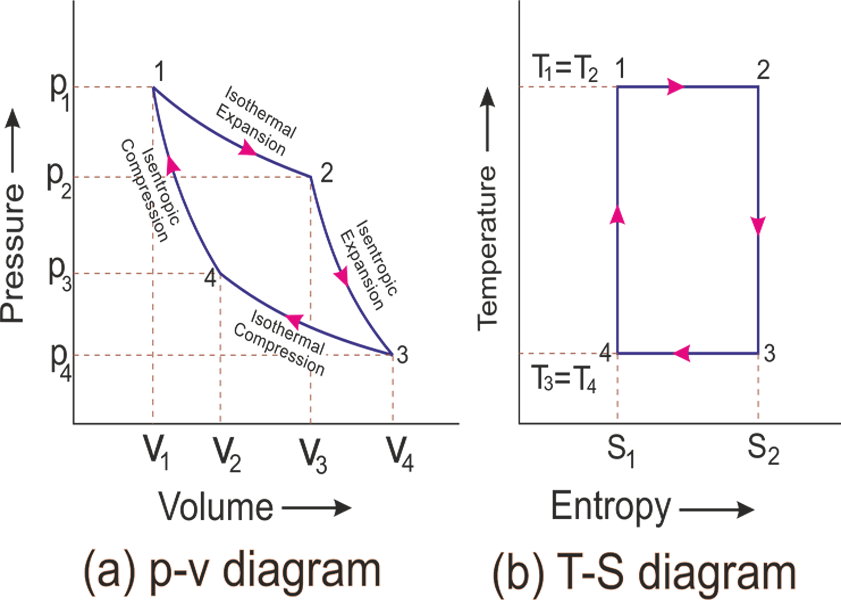
- Isothermal heat transfer: hot reservoir to working fluid at \(T_h\).
- Adiabatic expansion of working fluid to \(T_c\).
- Isothermal heat transfer: working fluid to cold reservoir at \(T_c\).
- Adiabatic compression of working fluid to \(T_h\).
label the figure with heat and work flows
Carnot Efficiency
 \[W = Q_h -
Q_c = Q_h\left(1-\frac{Q_c}{Q_h}\right)\] \[Q_c = T_cΔS_c,\,\,\,\,\, Q_h = -T_hΔS_h\]
\[W = Q_h\left(1-\frac{T_cΔ S_c}{-T_hΔ
S_h}\right)\] For a reversible process, \(Δ S_c = -Δ S_h\), so
\[W = Q_h -
Q_c = Q_h\left(1-\frac{Q_c}{Q_h}\right)\] \[Q_c = T_cΔS_c,\,\,\,\,\, Q_h = -T_hΔS_h\]
\[W = Q_h\left(1-\frac{T_cΔ S_c}{-T_hΔ
S_h}\right)\] For a reversible process, \(Δ S_c = -Δ S_h\), so
\[W = Q_h\left(1-\frac{T_c}{T_h}\right),\,\,\,η=\left(1-\frac{T_c}{T_h}\right)\]
Work from Heat Transfer: simple configuration

- Consider heat transfer between two objects.
- The two objects constitute the system.
- objects have constant and equal heat capacities \(C\),
- fixed volumes.
- Heat is exchanged and work is extracted from the system.
- Find the maximum work.
Work from Heat Transfer: analysis
\[ΔU_{sys} = -W\] \[ΔU_{sys} = ΔU_h + ΔU_c = c(T_i - T_h) + c(T_i - T_c)\]\[\frac{W}{C} = T_h + T_c - 2T_i\]
Work is maximized when \(T_i\) is minimized.
Find intermediate temperature
Work from Heat Transfer: analysis
Find intermediate temperature
For a given object, \(dU = TdS - \cancelto{0}{PdV}\) \[dS = \frac{dU}{T} = C\frac{dT}{T},\] Integrate to give \[ΔS_h = C\ln(T_i/T_h),\,\,\,ΔS_c = C\ln(T_i/T_c),\] \[ΔS_{sys} = ΔS_h + ΔS_c,\] \[\frac{ΔS_{sys}}{C} = \ln(T_i/T_h) + \ln(T_i/T_c),\] \[T_i = \exp\left[\frac{Δ S_{sys}}{2C} + \frac{\ln(T_hT_c)}{2}\right]\]
Work from Heat Transfer: result
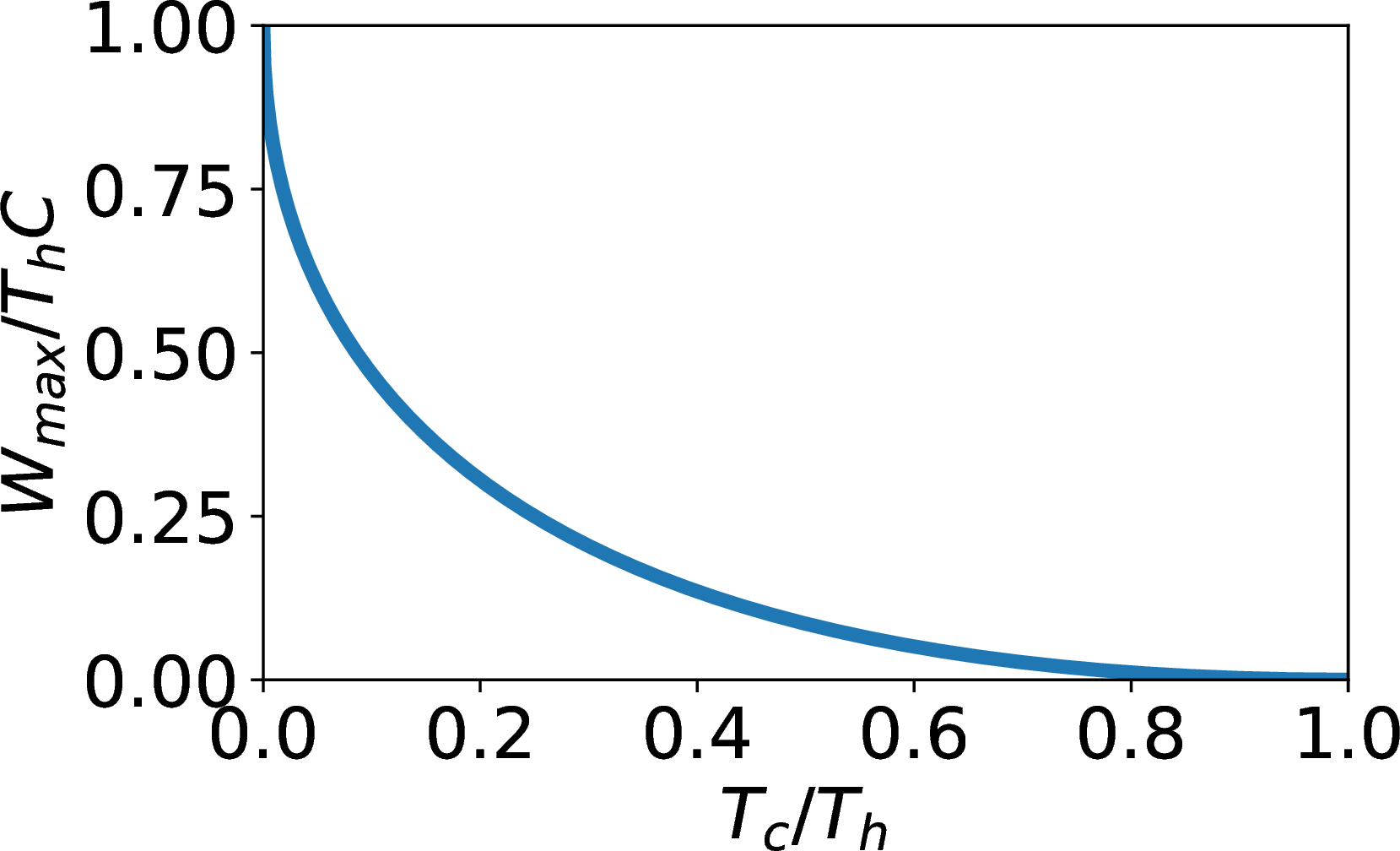
Again, \[T_i = \exp\left[\frac{Δ S_{sys}}{2C} + \frac{\ln(T_hT_c)}{2}\right]\] Max work for minimum \(T_i\). This occurs for minimum \(Δ S_{sys}\). \[Δ S_{sys}≥0→ \mbox{ take }Δ S_{sys}=0.\]\[T_i=\sqrt{T_hT_c},\] \[W_{max}/C = T_h + T_c - 2\sqrt{T_hT_c}\].
Work from Heat Transfer: efficiency
- \((W_{max}/C)_{max}=T_h\) at \(T_c=0\).
- \((W_{max}/C)_{min}=0\) at \(T_c=T_h\).
- Efficiency
- take the hot object as the driver
- normalize the work by \(Δ U_h\)
\[\begin{align}
η &= \frac{W/C}{Δ U_h/C}, \\
η &= \frac{T_h + T_c -
2\sqrt{T_hT_c}}{T_h-\underbrace{\sqrt{T_hT_c}}_{T_i}} =
1-\sqrt{\frac{T_c}{T_h}}.
\end{align}\]
\[η = 1-\sqrt{\frac{T_c}{T_h}}.\]
Work from Heat Transfer: process
Now, this whole development defines a change in state, not a process for achieving that state.
So, what is a process that can affect this change in state?
- Remember, we took \(Δ S_{sys}=0\), so this would need to be a reversible process.
- Reversible heat transfer is between objects at the same temperature.
Work from Heat Transfer: process
Start with gas at \(T_h\)
- Heat transfer between hot object and gas
- transfer a bit of heat from object to gas
- object \(T\) decreases a bit
- gas \(T\) increases a bit
- expand gas adiabatically till gas \(T\) drops to the object \(T\)
- repeat until \(T_h→ T_i\), \(T_{gas}→ T_i\).
- transfer a bit of heat from object to gas
- Expand the gas adiabatically until \(T_{gas} = T_c\)
- Heat transfer between cold object and gas
- transfer a bit of heat, then compress gas.
- repeat until \(T_c→ T_i\), \(T_{gas}→ T_i\).
- As in step 2, compress gas adiabatically until \(T_{gas}=T_h\).
The gas starts and ends at the same temperature, and so is only an intermediate needed to achieve the transition.
These are like the 4 steps of the Carnot Cycle, but with non-constant temperatures.
Work from Heat Transfer: generalize
In our example, we went all the way to the final intermediate temperature \(T_i\).
What if we don’t go all the way? Say, \(T_h → T_{h2}\) and \(T_c→ T_{c2}\).
\[Δ U_{sys} = -W,\] \[Δ U_{sys} = Δ U_h + Δ U_c = C(T_{h2}-T_h) + C(T_{c2}-T_c),\] Combine: \[\frac{W}{C} = T_h + T_c - T_{h2}-T_{c2}\]
Work from Heat Transfer: generalize
For each obejct \(dU=TdS = CdT\). Integrate to \[\frac{Δ S_h}{C} = \ln(T_{h2}/T_h),\,\,\,\,\frac{Δ S_c}{C} = \ln(T_{c2}/T_c).\] Combine these to give \[\frac{Δ S_{sys}}{C} = \ln(T_{h2}/T_h) + \ln(T_{c2}/T_c).\] For maximum work, take \(Δ S_{sys}=0\), as before. This gives \(T_{h2}/T_h = T_{c}/T_{c2}\), or\[T_{c2} = T_cT_h/T_{h2}\,\,\,\,\,\rightarrow\] \[\frac{W}{C} = T_h + T_c - T_{h2} - \frac{T_cT_h}{T_{h2}}\]
Work from Heat Transfer: efficiency
\[η = \frac{W/C}{Δ U_h/C} = \frac{T_h + T_c - T_{h2} - \frac{T_cT_h}{T_{h2}}}{T_h-T_{h2}}\]
- When \(T_{h2}=T_i=\sqrt{T_cT_h}\), \(η = 1-\sqrt{T_c/T_h}\), as before.
- When \(T_{h2}=T_h\), \(η = 0/0\).
- Use L’Hopital’s rule.
\[η = 1-\frac{T_c}{T_h}\]
This is the Carnot efficiency
So, we expect the efficiency to be bounded as \[\left(1-\sqrt{T_c/T_h}\right) ≤ η ≤ \left(1-T_c/T_h\right)\]
Work from Heat Transfer: plot
Parameterize \(T_{h2}\), which varies from \(T_h\) to \(\sqrt{T_cT_h}\), using progress variable \(ξ\): \[T_{h2} = T_h(1-ξ) + \sqrt{T_cT_h}(ξ)\] Insert into the expression for \(η\) \[η = \frac{r + ξ(1-\sqrt{r}) - \frac{r}{1-ξ+ξ\sqrt{r}}}{ξ(1-\sqrt{r})},\] where \(r = T_c/T_h\).
 The Carnot efficiency
is achieved when heat transfer occurs to and from infinite reservoirs,
whose temperature does not change during the heat transfer.
The Carnot efficiency
is achieved when heat transfer occurs to and from infinite reservoirs,
whose temperature does not change during the heat transfer.
Or, between finite objects, when very little heat transfer is allowed to occur, so that the object temperatures effectively don’t change.